Cuckoo!
0%

CS205 C/C++ Project02设计报告 简易计算器

Posted on In
支持输入算式的计算器，高精度，自定义变量，用户友好

Part 0. 团队成员

姓名 学号 贡献率
咕桃 - 100%

Part 1 - Analysis

题目重述&主要思路

本题目要求实现一个带有变量存储功能，支持基本运算和部分函数的计算器。

根据题目描述，本题的主要要求为：

  1. 带括号的复合算式的计算
  2. 可以设置并代入用户自定义变量
  3. 部分数学常用函数
  4. 高精度
  5. 使用Cmake管理项目

本项目使用了Project1中实现的BigNum高精度浮点数结构体进行数据的存储和运算，除完成上述全部基础要求外，本项目支持以下内容：

  1. 交互式输入输出
  2. sqrt(), exp(), ln(), sin(), cos() 五种常用函数（可轻易扩展更多）
  3. 支持多种形式的输入数据
  4. INF/NaN结果反馈
  5. 设定运算结果精度
  6. 查看/编辑变量列表
  7. 用户友好的帮助菜单

模型假设

由于题目所给信息较少，笔者对输入的数据范围等进行了假设，并根据假设设计程序。

以下是本程序适配的数据范围：

对于一个科学计数法浮点数，格式记为$A.BeC$

整数部分$A$与小数部分$B$位数之和记为$len$，$1\leq n \leq 10^{4}$，即存储一万位有效数字

10的幂指数$C$记为$exp$，$-10^{18}\leq exp \leq 10^{18}$，即存储上限为$10^{10^{18}}$量级

二元运算

本项目沿用了用高精度浮点数的存储方式，为了良好的扩展性采用了重载运算符的写法，较函数写法更为简洁，且基本运算的实现也和传统方式有所不同。

加法/减法

此种存储数据的好处在于可以将末尾0全部存储在$exp$变量中而非占用数组长度，但在进行加减法时需要进行对齐，对齐的思路为：

结果沿用两数中较小的$exp$，通过补0的方式对齐两数，避免了展开全部末尾0再运算带来的不必要时间和空间浪费，并在加减法完成后即时回收末尾0至$exp$中，最大地减少了空间开销。

加减法的具体逻辑较为常见，仅作简述：

  1. 较短数补0对齐
  2. 从低位起逐位加/减，并用carry/borrow标签模拟进位/借位
  3. 回收末尾0，规范化结果

乘法

沿用此前实现的$O(n^2)$高精度乘法，不作赘述。

除法

由于除法在绝大多数情况下会出现“除不尽”的无限循环小数的情况，本项目对输出结果进行了精度预设，当结果总长度达到200时停止运算（该参数可以通过big_num.h中的DIVIDE_PRECISION常量进行更改）。

以下是除法的具体逻辑，对于除法运算$A/B=C$：

  1. 将$A$和$B$调整至$B\leq A<10*B$

​ 由于特殊的数据存储方式，10的次方间的除法可以直接通过$exp$降次为long long类型的加减法，作差后存储于结果。

  1. 迭代计算后续位数

​ 重复执行以下操作：从$A$中减去若干次$B$并计数，直到$A<B$，得到$floor(A/B)$，将其存入结果中，将$A$扩增10倍，再次从中减去若干次$B$…理论而言，如此循环可以得到任意多位数的结果。

  1. 将结果倒序

​ 由于除法计算时，是从高位到低位产生结果，因此在结束运算后需要根据位数进行结果的倒序。

整数幂

实现了乘法和除法，就少不了快速幂。

快速幂的思路如下，对于乘方运算$A^B$：

将$B$用二进制表示，从低到高第i位为1代表$B$做拆解为2的次幂和之后有$2^{i-1}$的一项，该项在总运算中是一个因子：$A^{2^{i-1}}$，因此可以通过不断将底数$A$做平方，在$B$的二进制对应位为1时将此时的$A^{2^{i-1}}$乘进结果中，将乘法由$n$级别降为$logn$级别。

然而本项目中高精度数据十进制下就有$1e4$位，转成二进制将会更加痛苦，且丧失了原有的空间复杂度优势。考虑到我们每次计算时，暂时并不关心除了最低位以外的数，此处采用了将个位数和1做按位与的操作：若一个大整数$exp=0$且最低位为奇数，说明其二进制表达下最低位为1，单次判断操作时空复杂度都是O(1)。

小数幂

经过若干次不同的尝试，小数幂最终使用Math库中的pow，以下是大致的尝试过程：

  • 思路一：完全手动重构

    1. 先实现$e^x$和$ln(x)$！

      在不使用小数幂的前提下，实现这两个函数听上去有点天方夜谭，但只能用整数幂意味着可以使用泰勒级数近似计算这两个函数，所需要的运算恰好是目前已经是实现的加、减、乘、除、整数幂。

      以下是两个函数的展开结果：

      $e^x=\sum_{i=0}^{\infty} \frac{x^i}{i!}=1+\frac{x}{1!}+\frac{x^2}{2!}+ \frac{x^3}{3!}+…$

      $ln(x+1)=\sum_{i=1}^{\infty}(-1)^{i-1}\frac{x^i}{i}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+…$

      上机跑了一下，发现计算ln(1.5)还算快速和精确，但计算ln(2)时非常慢，并且计算出的ln(3)大出天际，经验证发现，使用麦克劳林级数计算，越远离0结果越不精确，且在ln(2)之后增量不收敛，因此会得出错误的结果。

    2. 调整收敛式

      $t=\frac{x-1}{x+1},ln(x)=ln(1+t)-ln(1-t)=2\sum_{i=0}^{\infty}\frac{t^{2i+1}}{2i+1}$

      通过引入$t$间接计算，将ln中的数字控制在了0~2之间，一定程度上提高了精确度，但此时程序为了计算函数，运行的时间已经不可忽略：乘法是$O(n^2)$，整数幂和除法都要多次调用乘法，为了结果的精度，级数的项数也需要设置在较高的水平。

    3. 曲折地实现小数幂

      既然不能直接算小数幂，我们可以将问题归纳为现有运算可以解决的形式：$A^B=e^{B*ln(A)}$

      即先对底数$A$求对数，与指数$B$相乘后再求自然指数。理论而言，由此可以只通过级数运算得到任意小数幂。

    4. 实际情况

      太慢，牺牲精度了还是太慢。在实现运算后，我尝试着运行了2^0.5，并经过多番痛截精度后，程序很忠诚地在15s左右给出了答案，经比对，精确到小数点后10位。

      原来的算法对于越大的数，计算起来的耗时是高次幂多项式增长的，因此程序几乎无法对大数进行小数幂运算。

      经过慎重考虑，我认为对于题设所需的计算器而言，具有一定精度而非常高效的Math库内置pow应该更加适合，因此有了以下的思路二。

  • 思路二：使用Math库内置pow

    1. double？

      库函数预设的参数类型为double类，虽然不是无限精度，但$[-1.7E308,1.7E308]$和小数点后15位的精度对于题设的绝大多数情况而言还是较为充足的，均衡时间和空间成本不失为一个优解。

      然而使用库函数需要将BigNum类转化为double类，利用库函数得出double类结果后仍要转化回BigNum以便后续的高精度计算。此处就涉及到两种类型的转换：

      1. BigNum→double

        这种情况，对于超出double范围的大数而言并不可行，但$[-1.7E308,1.7E308]$范围内，将BigNum中逐位存储的数取出，再根据exp改变double的小数点位置即可，此时小数点后的精度会有一定损失。

      2. double→BigNum

        本项目由于先前实现了良好的string转BigNum构造器，此处利用stringstream将double直接转为string型，再利用构造器即可无精度损失地将double转换为BigNum类。

    2. 效果？

      经验证，调用Math库函数进行运算后，运算时间又回到了肉眼可以忽略的量级，精度达到小数点后15位，说明优于原先完全重构的实现方法。

    3. 后续

      由此，吸取了上述颠沛流离过程的经验，本项目在后续引入函数的过程中，涉及到手动实现函数的时间/空间不可接受的情况时，采用了Math库的内置函数，更加简洁高效，也避免了使用自己造出来的方轮子带来的不便。

后缀表达式

又称逆波兰表达式，通过引入栈和队列改变操作数和操作符的顺序，得到后缀表达式辅助运算，常用于多种优先级的运算符同时存在的算式的求值，由于该算法普及性较好，老师想必也看了几十篇类似的讲解了，此处仅作简单的阐述：

  1. 确定符号优先级

    此处，参与运算需要区分先后顺序的有：括号，5种二元算符，函数。

    运算优先级如下：括号>函数>乘方>乘除>加减

  2. 中缀表达式→后缀表达式

    根据符号，将一整行字符串split成若干子串，从左到右读入中缀表达式：

    • 读入数字，直接加入队列
    • 读入操作符
      • 当前操作符为(，直接入栈
      • 当前操作符为)，持续出栈至队列中，直到将一个(出栈后停止
      • 当前操作符优先级高于栈顶，直接入栈
      • 当前操作符优先级不高于栈顶，持续出栈至队列中，直到当前操作符优先级高于栈顶后再入栈

    中缀表达式读入完毕后，若栈非空，则依次出栈加入队列中。

  3. 计算后缀表达式

    从后缀表达式队列中依次取出元素：

    • 读入数字，直接入栈
    • 读入操作符，取出栈顶两个元素进行二元运算(两个元素需要倒序)，运算结果再次入栈
    • 读入函数，取出栈顶单个元素代入运算，结果再次入栈

    后缀表达式运算完毕后，将栈中唯一元素出栈，即所求结果

变量

本项目使用STL::map简洁地实现了变量功能，读入命令后利用正则表达式匹配等式格式，检查合法后将左式作为变量名以字符串形式存储，右式依然是支持多种输入格式的高精度数字。

对于有一定精度要求的$\pi$和$e$，程序也预先将其内置在变量表中。

查看当前变量列表时，活用auto型迭代器遍历map；编辑变量时，对map删除再建立映射即可。

参与运算时，变量在中缀转后缀的过程中会被自动替换为其BigNum类键值参与运算，对于变量名相互包含的情况，本项目会取匹配的最长的变量名进行运算。

Part 2 - Code

项目结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
CPP\PROJ02
│  better_calc
│  CMakeLists.txt
│  report.pdf
│
├─inc
│      big_num.h
│      functions.h
│      varia.h
│
└─src
        func.cpp
        main.cpp
        operators.cpp
        RPN.cpp
        utils.cpp
        variables.cpp

main.cpp为运行主函数，可执行文件为：./better_calc，为实现交互式输入输出，本项目未使用命令行输入。

big_num.h为高精度浮点数头文件，其操作符重载实现位于operators.cpp，过程中使用的函数实现位于utils.cpp，逆波兰表达式的处理和求值位于RPN.cpp。

functions.h为数学函数头文件，其实现位于func.cpp。

varia.h为变量头文件，其实现和常用函数位于variables.cpp。

二元运算的重载

本节实现于operators.cpp，实现了加减乘除乘方五种二元运算的重载。

减法

加法与之类似，因此只放减法。

Step1. 通过讨论a,b的符号，将问题简化为a>b>0时的情况。

Step2. 排除其一为INF/NaN的情况，防止其影响计算

Step3. 对位数较少者进行补0

Step4. 逐位相减，模拟借位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
BigNum operator-(BigNum a, BigNum b)
{
    if (a.type == NaN || b.type == NaN)
    {
        return a.type == NaN ? a : b;
    }
    a = standardize_exp(a);
    b = standardize_exp(b);
    BigNum c = BigNum();
    if (a.sign)
    {
        if (b.sign)
        {
            c.sign = b < a;
        }
        else
        {
            b.sign = true;
            return a + b;
        }
    }
    else
    {
        if (b.sign)
        {
            b.sign = false;
            return a + b;
        }
        else
        {
            a.sign = true;
            b.sign = true;
            return b - a;
        }
    }
    if (a < b)
    {
        return -(b - a);
    }
    else if (a == b)
    {
        if (a.type == INF || b.type == INF)
        {
            return a.type == INF ? a : b;
        }
        return BigNum();
    }
    else
    {
        if (a.type == INF)
        {
            return a;
        }
        if (b.type == INF)
        {
            b.sign = false;
            return b;
        }
        if (a.exp >= b.exp)//a后补0
        {
            c.sign = true;
            c.exp = b.exp;
            c.len = a.len + a.exp - b.exp;
            for (int i = 1; i <= a.len; i++)
            {
                c.val[i + a.exp - b.exp] = a.val[i];
            }
            int borrow = 0;
            for (int i = 1; i <= c.len; i++)//给a补0
            {
                if (c.val[i] < borrow + b.val[i])
                {
                    c.val[i] = c.val[i] + 10 - borrow - b.val[i];
                    borrow = 1;
                }
                else
                {
                    c.val[i] -= borrow + b.val[i];
                    borrow = 0;
                }
            }
            c = standardize_exp(c);
            return c;
        }
        else//b后补0
        {
            c.sign = true;
            c.exp = a.exp;
            c.len = a.len+1;
            for (int i = 1; i <= c.len; i++)
            {
                c.val[i] = a.val[i];
            }
            int borrow = 0;
            for (int i = 1; i <= b.len+1; i++)
            {
                if (c.val[i + b.exp - a.exp] < borrow + b.val[i])
                {
                    c.val[i + b.exp - a.exp] = c.val[i + b.exp - a.exp] + 10 - borrow - b.val[i];
                    borrow = 1;
                }
                else
                {
                    c.val[i + b.exp - a.exp] -= borrow + b.val[i];
                    borrow = 0;
                }
            }
            c = standardize_exp(c);
            return c;
        }
    }
}

除法

Step1. 预处理INF/NaN的情况

Step2. exp作差，调整至b<a<10b

Step3. 在达到预设精度前不断扩增a得到更低位

Step4. 翻转数组，得到结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
BigNum operator/(BigNum a, BigNum b)
{
    if (is_zero(b))
    {
        BigNum err = BigNum();
        err.sign = !(a.sign xor b.sign);
        err.type = is_zero(a) ? NaN : INF;
        return err;
    }
    BigNum c = BigNum();
    c.sign = !(a.sign xor b.sign);
    a.sign = b.sign = true;
    c.exp = a.exp - b.exp;
    c.len = 0;
    a.exp = 0;
    b.exp = 0;
    if (a < b)//扩大a直到a>b
    {
        while (a < b)
        {
            a.exp++;
            c.exp--;
        }
    }
    else
    {
        b.exp++;
        if (b < a)//缩小a直到a<10b;
        {
            while (b < a)
            {
                a.exp--;
                c.exp++;
            }
        }
        b.exp--;
    }//现在是10b>a>b的情况
    while (c.len < DIVIDE_PRECISION)
    {
        int q = 0;
        while (!(a < b))
        {
            a = a - b;
            q++;
            a = standardize_exp(a);
        }
        c.val[++c.len] = q;
        a.exp++;
        a = standardize_exp(a);
        c.exp--;
        if (is_zero(a))
        { break; }
    }
    c.exp++;
    for (int i = 1; i <= (c.len >> 1); i++)
    {
        swap(c.val[i], c.val[c.len - i + 1]);
    }
    return c;
}

乘方

Step1. 预处理

Step2. 若为整数幂，使用高精度快速幂

Step3. 若为小数幂，使用pow()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
BigNum operator^(BigNum a, BigNum b)
{
    bool nega_pow = b.sign;
    b.sign=true;
    if (is_zero(a))
    {
        return BigNum();
    }
    if (is_zero(b))
    {
        return BigNum(1);
    }
    if (a.type == INF)
    {
        return a;
    }
    a = standardize_exp(a);
    b= standardize_exp(b);
    if(b.exp>=0)
    {
        BigNum res = BigNum(1);
        while(!is_zero(b))
        {
            res=shorten(res,1000);
            if((b.val[1]&1)&&(!b.exp))
            {
                res=res*a;
            }
            a=a*a;
            a=shorten(a,1000);
            b=b/BigNum(2);
            b= shorten(b,b.len+b.exp);
        }
        return nega_pow?res:(BigNum(1)/res);
    }//整数，使用快速幂
    else
    {
        //cout<<"float power"<<endl;
        return to_BigNum(exp(to_double(b)* log(to_double(a))));
    }
}

后缀表达式的转化和计算

本节实现于RPN.cpp，主要实现了两个功能，具体原理上文已述：

  1. 将中缀表达式转化为后缀表达式
  2. 计算后缀表达式

由于队列和栈中元素可能是操作符/函数/数字，因此开玩笑式的建立了aUtO结构体，作为栈和队列的类型，以实现不同类型的数据可以用同一个数据结构存储的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
struct aUtO//just kidding :)
{
    BigNum v;
    string s;
    bool is_num;
    
    aUtO(BigNum v)
    {
        this->v = v;
        is_num = true;
    }
    aUtO(string s)
    {
        this->s = s;
        is_num = false;
    }
    aUtO()
    {
        this->s = "";
        is_num = false;
    }
};

BigNum calculate(string s)
{
    trim(s);
    vector<string> sub;
    string it = "";
    for (char i: s)
    {
        if (is_operator(i)&&!(it[it.length()-1]=='e'&&i=='-'))
        {
            if (it != "")
            {
                sub.push_back(it);
                it="";
            }
            sub.push_back(string(1,i));
        }
        else
        {
            it += string(1,i);
        }
    }
    if(it!="")
    {
        sub.push_back(it);
        it="";
    }
    queue<aUtO> q;
    stack<aUtO> stk;
    for (string i: sub)
    {
        if (i.length() == 1 && is_operator(i[0]))
        {
            if (i == "(")
            {
                stk.push(aUtO(i));
                continue;
            }
            else if (i == ")")
            {
                while (stk.top().s != "(")
                {
                    q.push(stk.top());
                    stk.pop();
                }
                stk.pop();
                continue;
            }
            else
            {
                while (!stk.empty() && priority(i) <= priority(stk.top().s))
                {
                    q.push(stk.top());
                    stk.pop();
                }
                stk.push(aUtO(i));
                continue;
            }
        }
        else if (is_func(i))
        {
            while (!stk.empty() && priority(i) <= priority(stk.top().s))
            {
                q.push(stk.top());
                stk.pop();
            }
            stk.push(aUtO(i));
        }
        else if (classifier(i) != NaN)
        {
            q.push(aUtO(BigNum(i)));
        }
        else if (contains(i))
        {
            q.push(aUtO(value_of(i)));
        }
        else
        {
            BigNum err = BigNum();
            err.type = NaN;
            return err;
        }
    }
    while (!stk.empty())
    {
        q.push(stk.top());
        stk.pop();
    }
    BigNum x, y;
    aUtO cur, tmp;
    while (!q.empty())
    {
        cur = q.front();
        q.pop();
        if (cur.is_num)
        {
            stk.push(cur);
        }
        else
        {
            x = stk.top().v;
            stk.pop();
            if (is_operator(cur.s[0]))
            {
                y = stk.top().v;
                stk.pop();
                stk.push(calc(y, x, cur.s[0]));
            }
            else if (is_func(cur.s))
            {
                if(cur.s=="exp")
                {
                    stk.push(aUtO(to_BigNum(exp(to_double(x)))));
                }
                else if(cur.s=="ln")
                {
                    stk.push(aUtO(to_BigNum(log(to_double(x)))));
                }
                else if(cur.s=="cos")
                {
                    stk.push(aUtO(to_BigNum(cos(to_double(x)))));
                }
                else if(cur.s=="sin")
                {
                    stk.push(aUtO(to_BigNum(sin(to_double(x)))));
                }
                else if(cur.s=="sqrt")
                {
                    stk.push(aUtO(to_BigNum(sqrt(to_double(x)))));
                }
            }
        }
    }
    return stk.top().v;
}

级数近似计算函数

本节代码位于func.cpp，由于中途易辙，此处实现了自然指数和自然对数两个函数。

虽然最后决定弃用，但此处仍展示其思路。

大致流程为：预处理→计算级数求和→得到结果。

从运算复杂度而言，这两个函数的实现对于时间的耗费过大，并不适用于题设环境。

$e^x$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
BigNum exp(BigNum a)
{
    if (is_zero(a))
    {
        return BigNum(1);
    }
    if (a.type == INF || a.type == NaN)
    {
        return a;
    }
    BigNum res = BigNum(1);
    BigNum fac = BigNum(1);
    for (int i = 1; i <= PRECISION; i++)
    {
        BigNum it = BigNum(i);
        fac = fac * it;
        res = res + ((a ^ it) / fac);
    }
    return res;
}

$ln(x)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
BigNum ln(BigNum a)
{
    if (a == BigNum(1))
    {
        return BigNum(0);
    }
    if (!a.sign || is_zero(a))
    {
        BigNum err = BigNum();
        err.type = NaN;
        return err;
    }
    BigNum res = BigNum();
    BigNum t = (a - BigNum(1)) / (a + BigNum(1));
    for (int i = 1; i <= 2 * PRECISION; i++)
    {
        if (i & 1)
        {
            BigNum it = BigNum(i);
            res = res + BigNum(2) / it * t ^ it;
        }
    }
    return res;
}

因此，本项目的五个函数均取自Math库。

变量

以下是在varia.h头文件中的函数，基于STL::map实现，因此功能简洁明了，实现位于variables.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void trim(string &s);//去除空格

BigNum value_of(string name);//取值

void insert(string name, string val);//插入(输入参数为字符串)

void insert(string name, BigNum val);//插入(输入参数为BigNum)

bool remove(string name);//删除

bool modify(string name, BigNum val);//修改

bool contains(string name);//查询是否存在

int add(string s);//添加/编辑映射

void value_list(int precision);//打印变量列表

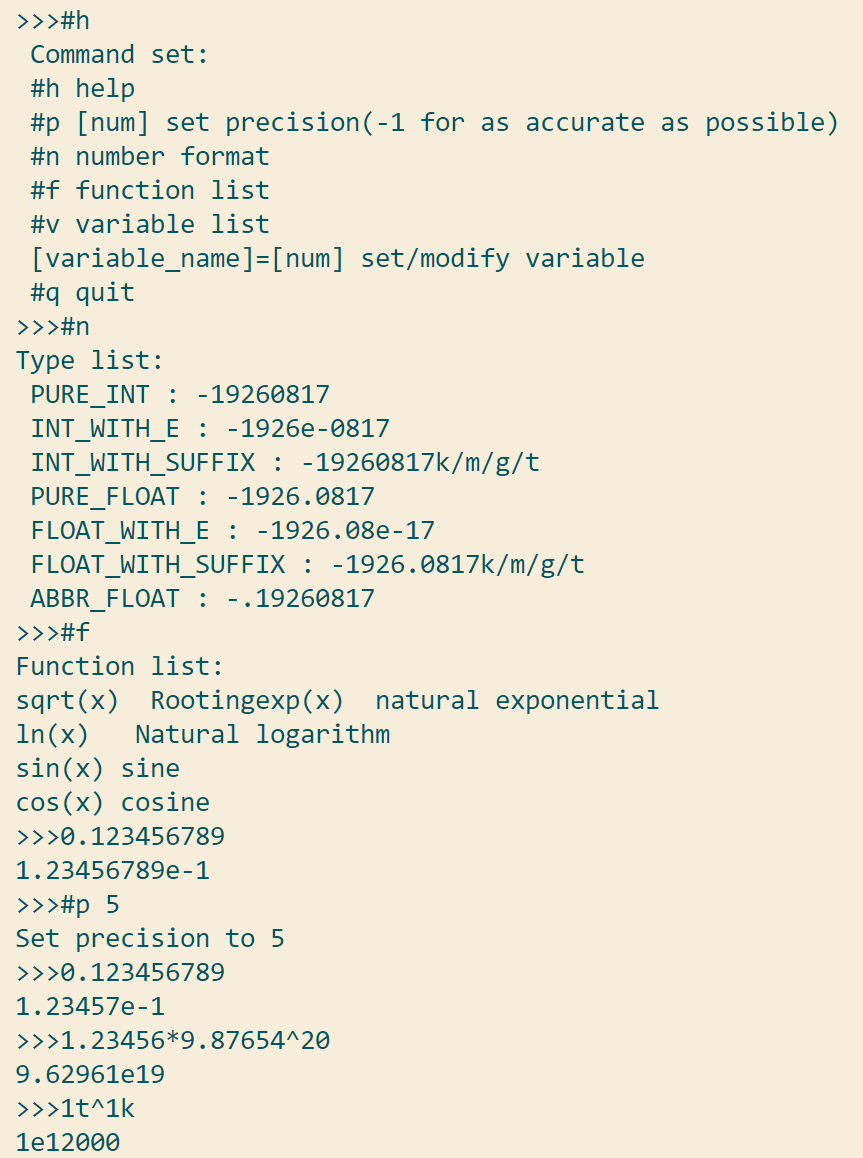
用户友好设计

本程序设计了用户友好的交互命令，命令列表如下：

1
2
3
4
5
6
7
#h help
#p [num] set precision(-1 for as accurate as possible)
#n number format
#f function list
#v variable list
[variable_name]=[num] set/modify variable
#q quit

分别实现了：帮助菜单、设置输出精度、显示支持的输入格式列表、显示支持的函数列表、当前变量列表、创建/编辑变量、退出功能，本项目使用交互式输入输出，在收到#q指令前可持续输入，并会对不同错误进行报错提示，并且使用了>>>来让计算器看起来比较像某种语言的交互式界面。

Part 3 - Result & Verification

经与计算器对照确认，下列结果均正确

Bunched Test case #1: 基础五则运算

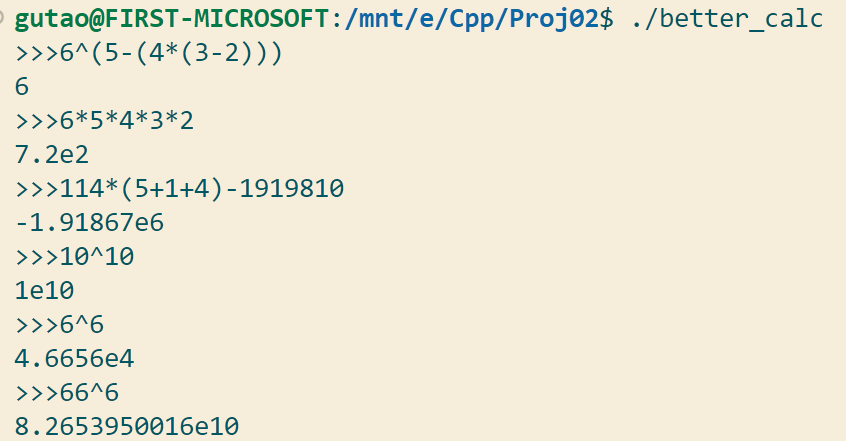
image-20221016015749671.png

Bunched Test case #2: 高精度五则运算

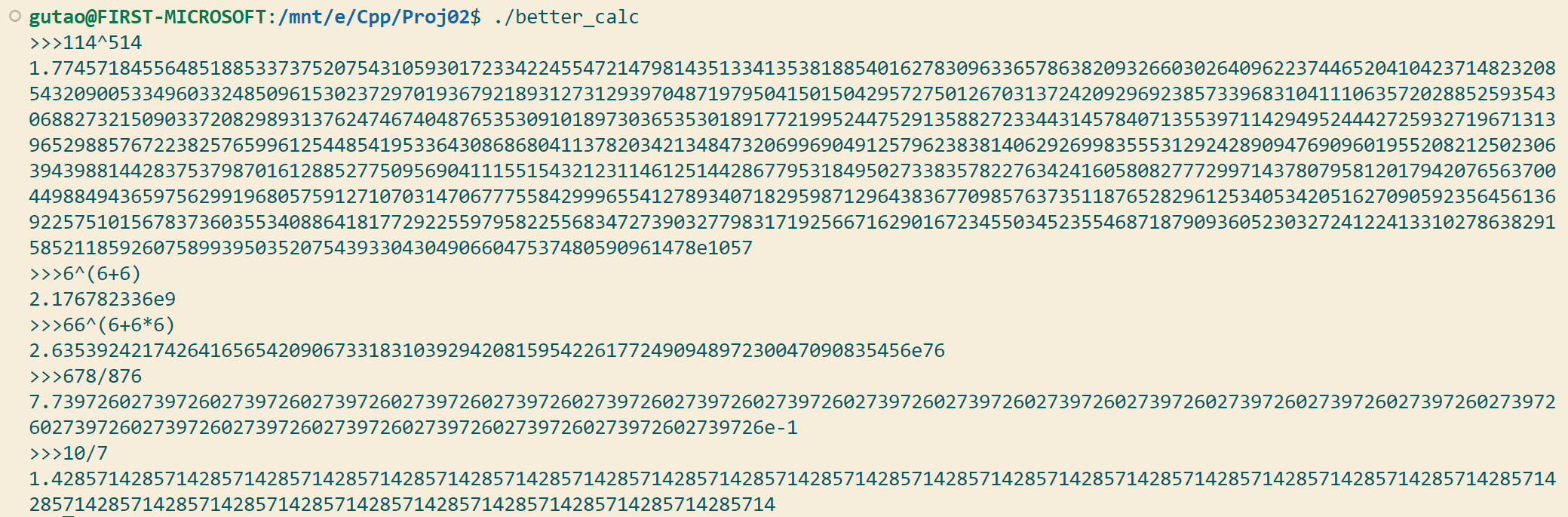
image-20221016020050214.png

Bunched Test case #3: 变量赋值与运算

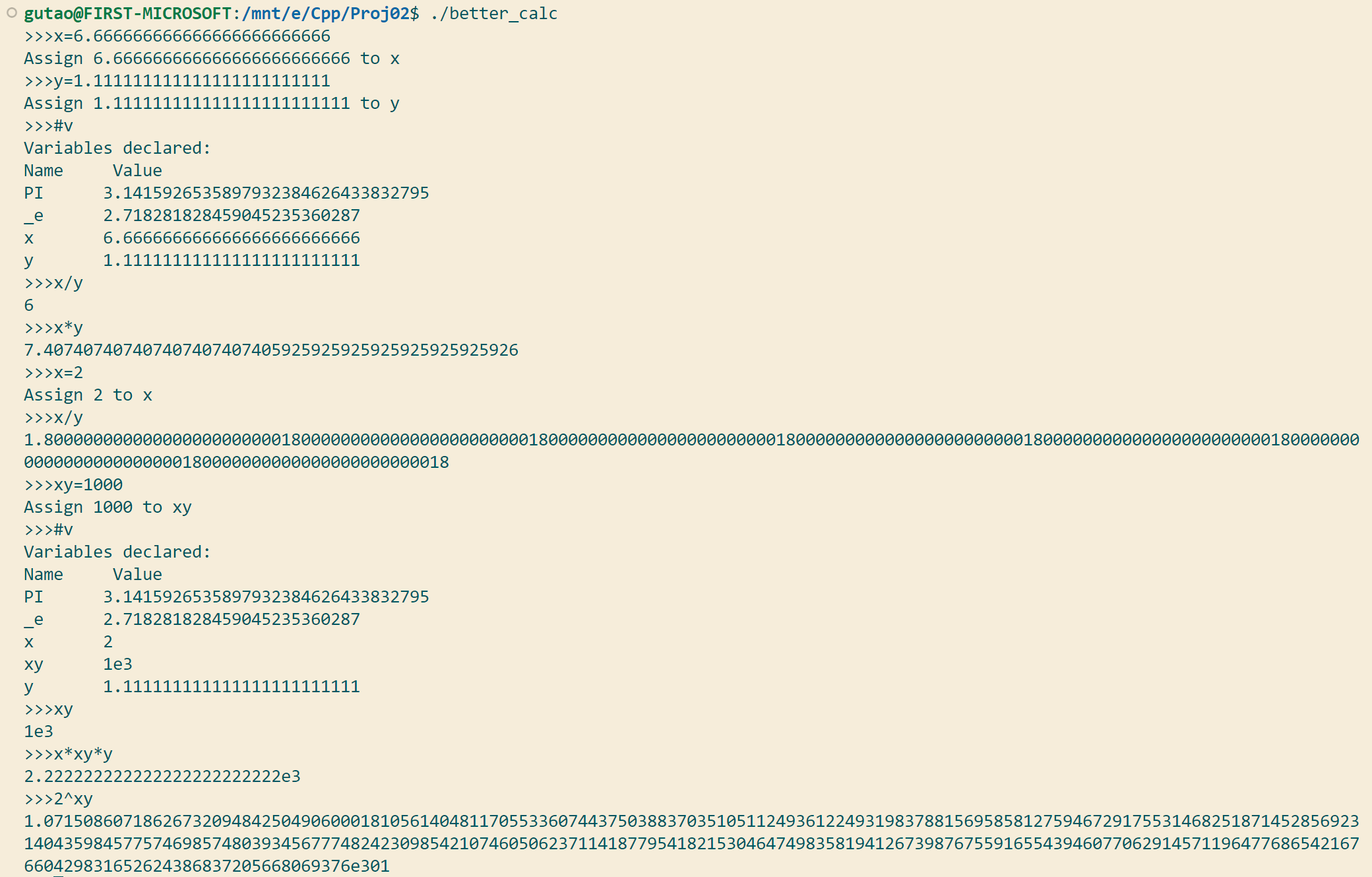
image-20221016020446449.png

Bunched Test case #4: 小数幂与函数

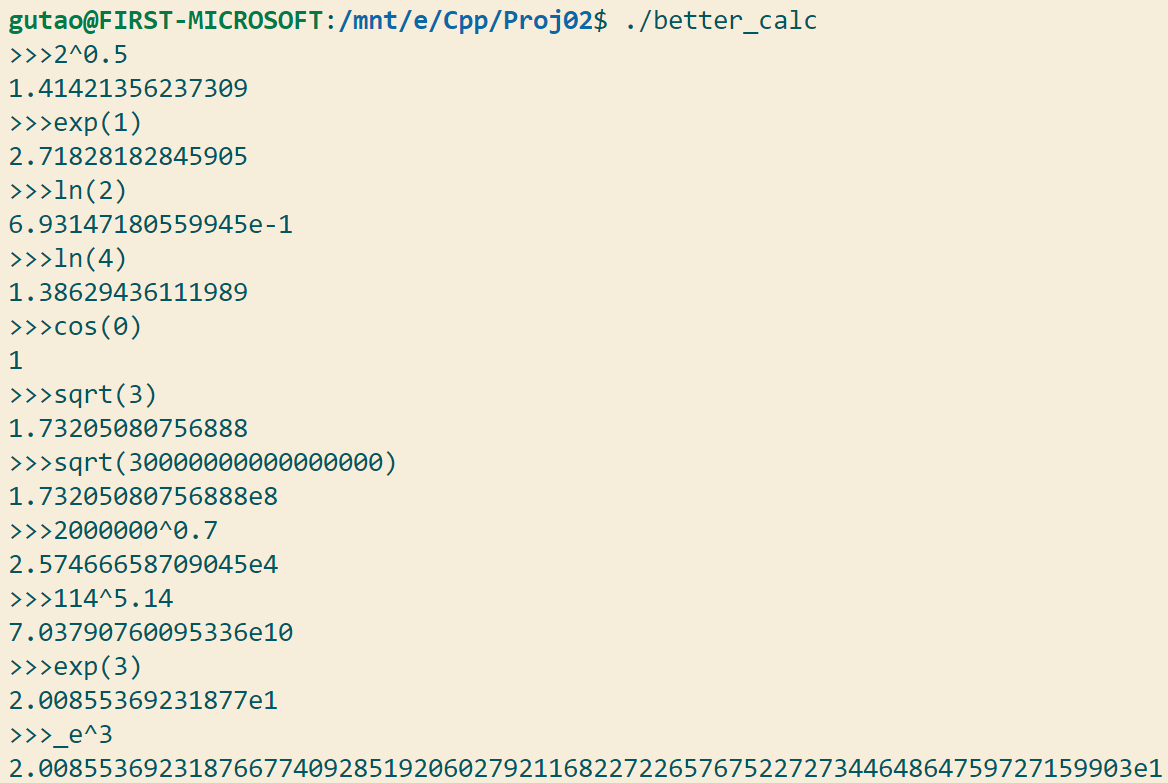
image-20221016021351071.png

Bunched Test case #5: 用户友好设计

image-20221016021628241.png

Part 4 - Difficulties & Solutions

重载运算符

Difficulty: 新形式存储在对齐小数点时需要新的方法，和传统写法有一定差异

Solution: 充分利用存了exp的优势，将按位运算简化为对exp的运算，补零对齐即可按常规思路模拟计算。

运算顺序

Difficulty: 含有括号、函数、五种二元运算的中缀表达式运算顺序难以用计算机模拟计算

Solution: 确定优先级，利用栈和队列辅助，转换成后缀表达式再使用固定流程循环计算。

变量

Difficulty1: 如何防止用户起奇怪的变量名？

Solution1: 用正则表达式进行诸如“第一位不能是数字”这样的限制，若不符条件报错即可。

Difficulty2: 在变量名相互包含的情况下如何代入？

Solution2: 根据运算符进行split，若算式合法，则分出来的一定是完整变量名，选整个完整变量名带入计算即可，若不存在该变量则说明变量列表没有。

小数次幂&函数

Difficulty: 对于以$O(n^2)$实现的模拟乘法作为基础编写的整数幂和除法时间复杂度只会比$O(n^2)$高出更多，如遇计算级数这样高频调用乘法的情景，这样的时间复杂度将显得过高。

Solution: 本项目选择引用Math库内置的函数进行计算，高效简洁，避免重复造轮子(其实还是造了，只是技不如人，甘拜下风)。

Possible Solution: 其实后来有考虑过一个解决方案，就是将小数次幂的整数部分剥离，只计算小数部分，这样直观感觉上会极大降低计算耗时，但对自己的乘法没什么信心，于是没有再造方轮子。

Part 5 - Difficulties & Solutions

本次项目让我深刻的认识到了自己能力的有限：当可以做的事远大于自己所能做的事的时候。

重载完加减乘除的时候感觉还非常良好，写整数次幂的时候就开始纠结小数次幂该怎么写，想到级数展开的解法后怀着对时间复杂度的忐忑实现了，也非常不让人失望地耗时过长了。

回过头一想：double的精度其实挺够用的(如果把整数部分也用来存小数)，才发现自己走远了。

虽然完成了项目要求，但我认为仅仅是高精度这一个算法就还有无数值得我去了解的内容，何况是C++这一整门课呢？

个人很喜欢这种能够用10~20小时左右做一个小项目的形式，耐心、心性和debug能力都有了显著的磨练和提升。