出处:CLRS Problem 32-1,DSAA(H) 2021 Fall Midterm Final Problem
题目描述
记$y^i$为字符串$y$进行$i$次重复后的拼接字符串,例如$(ab)^3=ababab$。
对于字符串$x\in\Sigma^{\star}$,若存在字符串$y\in\Sigma^{\star}$和正整数$r$,使得$x=y^r$,则称$r$为$x$的一个重复因子。
记$\rho(x)$为字符串$x$的最大重复因子。
设计算法对于输入字符串$P[1_\cdots m]$,对于$1\leq i\leq m$,求解$\rho(P[1_\cdots i])$,即$P$每个前缀串的最大重复因子。
记$\rho^{\star}(P)=max\{\rho(P[1_\cdots i])\}, 1\leq i\leq m$,即$P$所有前缀串中最大重复的因子。
证明:从长度为$m$的二进制串集合中任取其一,则$\rho^{*}(P)$的期望值是$O(1)$的。
证明Galil & Seiferas算法的正确性:
该算法能在$O(\rho^{\star}(P)n+m)$的时间内,从文本串$T[1_\cdots n]$中匹配模式串$P[1_\cdots m]$的所有出现位置,且除模式串和文本串外,空间开销仅为$O(1)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14REPETITION_MATCHER(P, T)
m = P.length
n = T.length
k = 1 + ρ*(P)
q = 0
s = 0
while s ≤ n - m
if T[s + q + 1] == P[q + 1]
q = q + 1
if q == m
print "Pattern occurs with shift" s
if q == m or T[s + q + 1] != P[q + 1]
s = s + max(1, ceil(q / k))
q = 0
算法设计
求出最长公共前后缀数组$\pi[m]$,记$k=m-\pi[m]$。
若$k|m$,则$k$就是最小循环节,$\rho(P)=\frac{m}{k}$。
$\pi[m]=0$的情况:除$P$本身外不存在循环节,$k=m$,显然$\rho(P)=1$成立。
$\pi[m]>0$的情况:由于$k|m$又$k≠m$,则$2k\leq m$,又有$\pi[m]\ge \frac{m}{2}$,因此最长公共前后缀有交集(如图)。
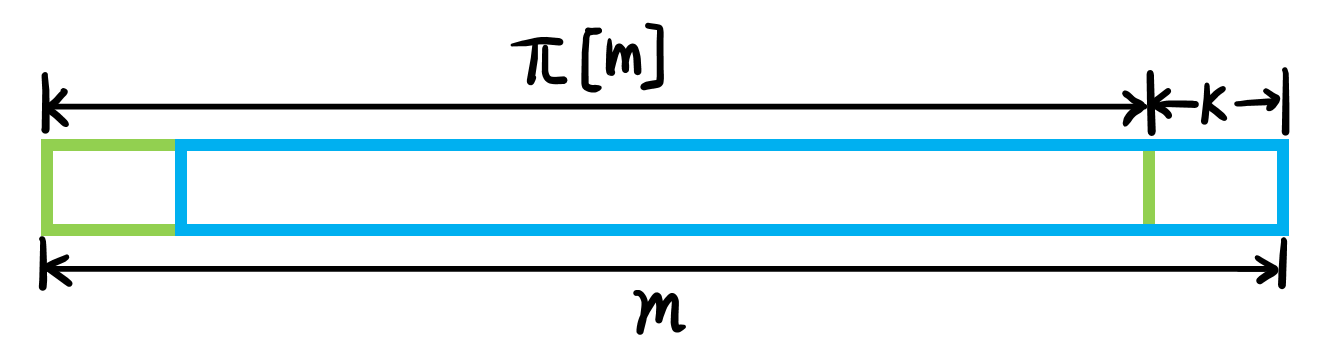
利用公共前后缀的性质,后缀(蓝色)的末尾$k$个字符与前缀的末尾$k$个字符相等,而前缀的末尾$k$个字符又是后缀(蓝色)的末尾倒数$k+1\sim2k$共$k$个字符,由此递推,由于$k|m$,有$k|\pi[m]$,末尾$k$个字符也就是$P$的循环节了。
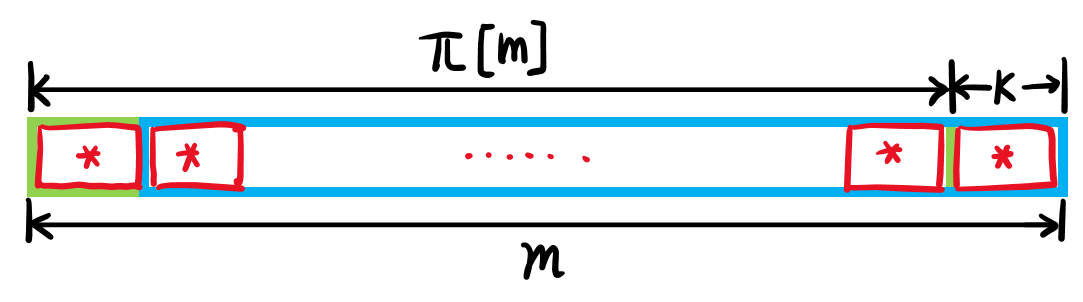
现用反证法证明不存在更小的循环节/更大的$\rho(P)$:若存在更小的循环节,则说明$P$最长公共前后缀可以更长($\pi[m]$可以更大),然而现在保证了$\pi[m]$的正确性,因而不存在更小的循环节。
若$k\nmid m$,则除$P$本身外不存在循环节,$\rho(P)=1$,证明如下:
假设$\rho(P)\ge2$,则说明$P$有至少重复两次的循环节,那么$P$最长公共前后缀应为恰好循环$\rho(P)-1$次的循环节,此时$k$应为单个循环节长度$\frac{m}{\rho(P)}$,则$k|m$,矛盾。
时间复杂度:求$\pi[m]$耗时$O(m)$,判断整除等运算均为$O(1)$,整体时间复杂度$O(m)$
期望值证明
$^\star$这里貌似怪怪的,不太懂概率上界为什么是4就能说明期望有界了。
$^\star$我感觉最后那个概率沿着这种思路应该不能粗暴相加要用容斥,现在没时间想先留个坑。
二进制串$P$的长度为$i$的前缀子串一共有$2^i$种。假设$r|i$,则可以构造长度为$\frac{i}{r}$的循环节,共有$2^{\frac{i}{r}}$种,选中概率为$\frac{2^{\frac{i}{r}}}{2^i}=\frac{1}{2^{i\frac{r-1}{r}}}$。则利用布尔不等式计算$\rho(P[1_{\cdots}i])> r$的概率为
接下来对于每个$i\in[1,m]$,用布尔不等式加和求$\rho(P)>r$的概率上界:
该式随$r$增长,较快地收敛到4,期望值是有界的且与$m$无关,因而为$O(1)$
Galil & Seiferas算法
This algorithm correctly finds the occurrences of the pattern $P$ for reasons similar to the Knuth Morris Pratt algorithm. That is, we know that we will only increase $q\ \rho^{\star}(P)$ many times before we have to bite the bullet and increase $s$, and $s$ can only be increased at most $n − m$ many times. It will definitely find every possible occurrence of the pattern because it searches for every time that the primitive root of $P$ occurs, and it must occur for $P$ to occur.