Part 0. 团队成员
项目结构 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 CS205_Project04 │ CMakeLists.txt │ README.md │ ├─build │ ├─doc │ Report.pdf │ ├─inc │ matmul.h │ matrix.h │ └─src benchmark.c matmul.c matrix.c
使用说明 运行本项目前,请预先安装OpenBLAS与OpenMP。您可以使用以下命令下载本项目:
1 $ git clone https://github.com/GuTaoZi/CS205_Project04.git
下载完成后,请在CMakeLists.txt中调整OpenBLAS目录,您也可以根据您的系统架构调整编译选项。
1 2 include_directories (/usr/local/include ./inc)link_libraries (/usr/local/lib/libopenblas.a)
使用以下命令编译、运行可执行文件matmul:
1 2 3 4 cd build cmake .. make ./matmul
Part 1 - Analysis 题目重述&主要思路 本题目要求使用C语言 实现正确而尽可能高效的矩阵乘法,使用OpenMP, SIMD等工具提升效率,并与OpenBLAS库中的矩阵乘法在各平台进行效率比较。
根据题目描述,题目要求的矩阵乘法需要支持的主要功能为:
实现朴素乘法,用于检验高效矩阵乘法的正确性
OpenMP, SIMD等工具实现提升效率的矩阵乘法测试$16\times16$、$128\times128$、$1k\times1k$、$8k\times8k$、$64k\times64k$等尺寸的矩阵乘法效率
与OpenBLAS进行效率比较
进行ARM等多平台效率测试
本项目完成了上述基础要求,并在其中几项进行了拓展,本次报告将侧重于矩阵乘法的优化过程,与上次报告重复处将略讲,详见下文。
模型假设 本项目按题设要求继承了前一项目的数据类型,在实现矩阵乘法时以效率为主,小幅降低了安全性检查的严格程度。
单个元素均为4字节float类型,有效位数默认为6位,数据范围约$-3.4\ast 10^{-38}<val<3.4\ast 10^{38}$
参与运算的矩阵均为方阵 ,且阶数为8的倍数
可接受<0.01的单精度浮点数计算误差
Part 2 - Code 宏与结构体 1 2 3 4 5 6 7 8 9 #define float_equal(x, y) ((x-y)<1e-3&&(y-x)<1e-3) typedef struct Matrix_ { size_t row; size_t col; float *data; } Matrix;
在题设条件下,矩阵尺寸默认$row=col$(其实可以存成一个,但部分矩阵乘法函数简单修改后可支持非方阵情况),使用size_t存储,满足跨平台需求。
使用浮点型指针指向存储数据,采用行优先方式存储,空间由创建函数动态分配,分配后可通过释放函数释放。
创建、释放与合法性检查 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Matrix *createMatFromArr (size_t row, size_t col,float *src) if (row==0 ||col==0 ) { fprintf (stderr, "Rows/cols number is 0.\n" ); return NULL ; } if (src==NULL ) { fprintf (stderr,"Source array is NULL.\n" ); return NULL ; } Matrix *pMatrix = malloc (sizeof (Matrix)); if (pMatrix == NULL ) { fprintf (stderr, "Failed to allocate memory for a matrix.\n" ); return NULL ; } pMatrix->row = row; pMatrix->col = col; pMatrix->data = malloc (sizeof (float ) * row * col); if (pMatrix->data == NULL ) { fprintf (stderr, "Failed to allocate memory for the matrix data.\n" ); free (pMatrix); return NULL ; } memcpy (pMatrix->data,src,sizeof (float )*row*col); return pMatrix; }
以从数组创建矩阵为例,本项目该部分与前一项目的差别在于:优化了安全性检查与报错,使用fprintf的stderr报错,使其变得更加合理和规范,同时采用了memcpy()代替手动赋值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 bool releaseMat (Matrix **pMatrix) if (pMatrix == NULL ) { fprintf (stderr,"Pointer to the pointer of matrix is NULL.\n" ); return false ; } if ((*pMatrix)==NULL ) { fprintf (stderr,"The pointer to the matrix is NULL.\n" ); return false ; } if ((*pMatrix)->data==NULL ) { fprintf (stderr,"The pointer to the matrix data is NULL.\n" ); return false ; } free ((*pMatrix)->data); free (*pMatrix); *pMatrix = NULL ; return true ; }
释放矩阵与此前的差别同样在与报错与安全性的优化。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 bool safe_check (Matrix *src1, Matrix *src2, Matrix *dst) if (src1 == NULL ) { fprintf (stderr, "File %s, Line %d, Function %s(): The 1st parameter is NULL.\n" , __FILE__, __LINE__, __FUNCTION__); return false ; } else if (src1->data == NULL ) { fprintf (stderr, "%s(): The 1st parameter has no valid data.\n" , __FUNCTION__); return false ; } if (src2 == NULL ) { fprintf (stderr, "File %s, Line %d, Function %s(): The 2nd parameter is NULL.\n" , __FILE__, __LINE__, __FUNCTION__); return false ; } else if (src2->data == NULL ) { fprintf (stderr, "%s(): The 2nd parameter has no valid data.\n" , __FUNCTION__); return false ; } if (dst == NULL ) { fprintf (stderr, "File %s, Line %d, Function %s(): The 3rd parameter is NULL.\n" , __FILE__, __LINE__, __FUNCTION__); return false ; } else if (dst->data == NULL ) { fprintf (stderr, "%s(): The 3rd parameter has no valid data.\n" , __FUNCTION__); return false ; } if (src1->row != src1->col || src1->row != src2->row || src1->col != src2->col || src1->row != dst->row || src1->col != dst->col) { fprintf (stderr, "The input and the output do not match, they should have the same square size.\n" ); fprintf (stderr, "Their sizes are (%zu,%zu), (%zu,%zu) and (%zu,%zu).\n" , src1->row, src1->col, src2->row, src2->col, dst->row, dst->col); return false ; } return true ; }
在进行矩阵乘法前,本项目对三个参数矩阵都进行了安全性检查,并用更规范的形式报错和处理。此处的最后一个if限定了三个矩阵应均为方阵,修改条件后可解除方阵要求。
矩阵乘法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 bool safe_check (Matrix *src1, Matrix *src2, Matrix *dst) bool matmul_plain (Matrix *src1, Matrix *src2, Matrix *dst) bool matmul_divide (Matrix *src1, Matrix *src2, Matrix *dst) bool matmul_omp (Matrix *src1, Matrix *src2, Matrix *dst) bool matmul_avx_vec8 (Matrix *src1, Matrix *src2, Matrix *dst) bool matmul_avx_block8 (Matrix *src1, Matrix *src2, Matrix *dst) bool matmul_thread (Matrix *src1, Matrix *src2, Matrix *dst, size_t num_threads)
项目实现了6个矩阵乘法函数,依次为:朴素乘法,4×4分块乘法,OpenMP优化朴素乘法,向量点乘级SIMD优化朴素乘法,SIMD优化8×8分块乘法,手动多线程算法(基于pthread.h)。
下文将逐个展开解析优化策略和原理,效率比较部分将在后文体现。
朴素乘法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 bool matmul_plain (Matrix *src1, Matrix *src2, Matrix *dst) if (!safe_check (src1, src2, dst)) { return false ; } size_t n = src1->row; for (size_t i = 0 ; i < n; i++) { size_t i_n = i * n; for (size_t k = 0 ; k < n; k++) { float t = src1->data[i_n + k]; size_t k_n = k * n; for (size_t j = 0 ; j < n; j++) { dst->data[i_n + j] += t * src2->data[k_n + j]; } } } return true ; }
说是朴素,但要是为了衬托其他算法把朴素写得太朴素没什么意思,所以这个朴素版其实是小幅优化后的朴素版,继承了上一项目的乘法,时间复杂度$O(N^3)$。
硬件优化:通过交换循环顺序将内存访问的跳跃次数从$n^3+n^2-n$降低到$n^2$次。
软件优化:暂存了$i×n$和$k×n$,小幅减少了乘法的次数。
4×4分块乘法(Tiling) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 bool matmul_divide (Matrix *src1, Matrix *src2, Matrix *dst) if (!safe_check (src1, src2, dst)) { return false ; } size_t n = src1->row; size_t k, j; float *data1 = src1->data; float *data2 = transpose (src2->data, n); float *data3 = dst->data; for (size_t i = 0 ; i < n; i += 4 ) { for (j = 0 ; j < n; j += 4 ) { for (k = 0 ; k < n; k += 4 ) { for (size_t i2 = 0 ; i2 < 4 ; i2++) { for (size_t j2 = 0 ; j2 < 4 ; j2++) { for (size_t k2 = 0 ; k2 < 4 ; k2++) { data3[(i + i2) * n + (j + j2)] += data1[(i + i2) * n + (k + k2)] * data2[(k + k2) + (j + j2) * n]; } } } } } } return true ; }
硬件优化:在大规模矩阵乘法时,两个元素间隔可能很远,因此CPU往往需要将两个元素都加载进cache,耗费大量访存时间。考虑到小矩阵的数据可以存储进CPU cache中,我们可以将原先的大矩阵按行和列切割成若干4×4的小块再进行运算。同时,通过转置矩阵将内存访问变得连续。
OpenMP优化朴素乘法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 bool matmul_omp (Matrix *src1, Matrix *src2, Matrix *dst) if (!safe_check (src1, src2, dst)) { return false ; } register size_t n = src1->row; register size_t k, j; #pragma omp parallel { #pragma omp for private(k, j) for (register size_t i = 0 ; i < n; i++) { size_t i_n = i * n; for (k = 0 ; k < n; k++) { float t = src1->data[i_n + k]; size_t k_n = k * n; for (j = 0 ; j < n; j++) { dst->data[i_n + j] += t * src2->data[k_n + j]; } } } } return true ; }
硬件优化:将原本串行执行的多次乘法通过OpenMP变为多线程并行,双线程效率较单线程折半,四线程较双线程接近折半,不过在线程数增加的过程中耗时减少的幅度逐渐降低,但总体而言较朴素算法有若干倍的提升,详见下文测试部分。
向量化SIMD优化 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 bool matmul_avx_vec8 (Matrix *src1, Matrix *src2, Matrix *dst) if (!safe_check (src1, src2, dst)) { return false ; } size_t n = src1->row; size_t k, j; float *data1 = src1->data; float *data2 = transpose (src2->data, n); float *data3 = dst->data; #pragma omp parallel for (size_t i = 0 ; i < n; i++) { #pragma omp for private(k, j) for (j = 0 ; j < n; j++) { __m256 sx = _mm256_setzero_ps(); for (k = 0 ; k < n; k += 8 ) { sx = _mm256_add_ps(sx, _mm256_mul_ps(_mm256_loadu_ps(data1 + i * n + k), _mm256_loadu_ps(data2 + j * n + k))); } sx = _mm256_add_ps(sx, _mm256_permute2f128_ps(sx, sx, 1 )); sx = _mm256_hadd_ps(sx, sx); data3[i * n + j] = _mm256_cvtss_f32(_mm256_hadd_ps(sx, sx)); } } return true ; }
由于计算对象矩阵默认阶数为8的倍数,因此可以将8个连续的元素使用__m256进行合并,再进行批量乘法。在使用了OpenMP并行优化的基础上,进行维数为8的向量乘法代替8次串行的逐元素运算,将效率再次大幅提高。
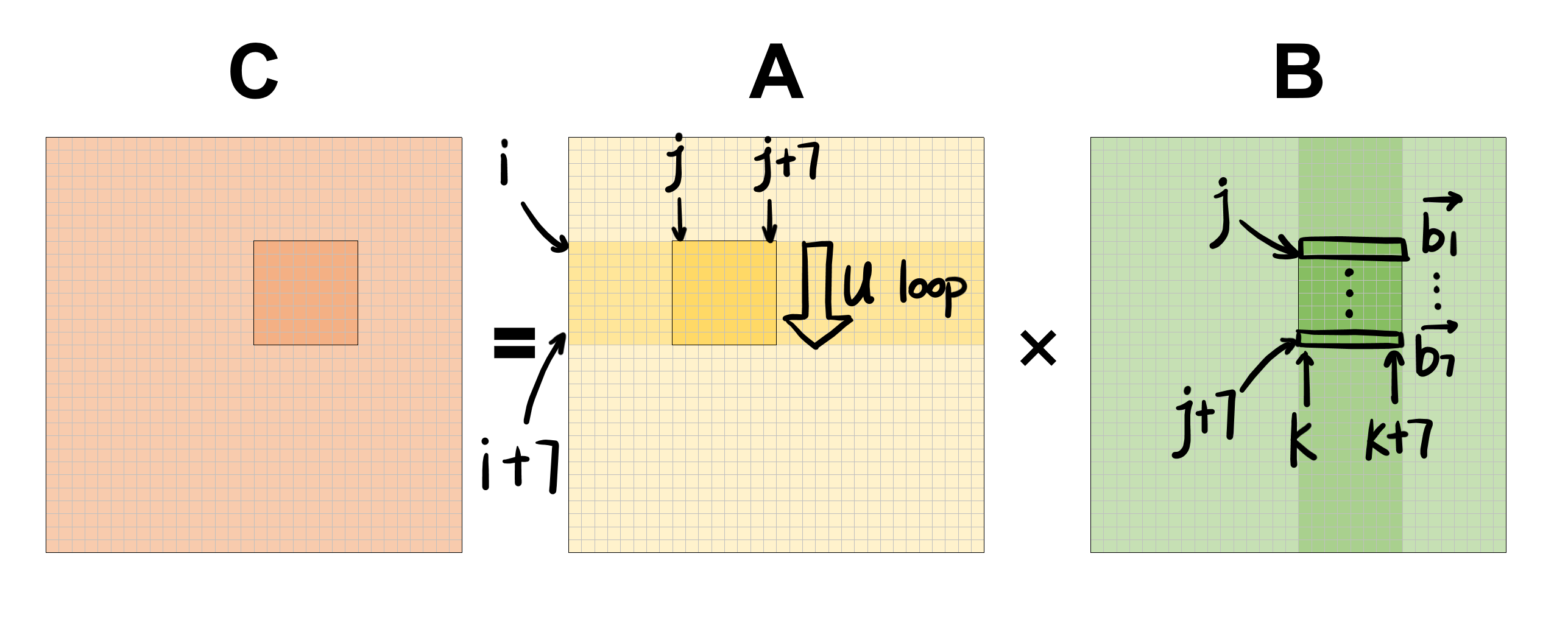
8×8分块SIMD优化 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 bool matmul_avx_block8 (Matrix *src1, Matrix *src2, Matrix *dst) if (!safe_check (src1, src2, dst)) { return false ; } register size_t n = src1->row; float *data1 = src1->data; float *data2 = src2->data; float *data3 = dst->data; #pragma omp parallel for for (register size_t i = 0 ; i < n; i += 8 ) { for (register size_t j = 0 ; j < n; j += 8 ) { for (register size_t k = 0 ; k < n; k += 8 ) { for (register size_t u = i; u < i + 8 ; u++) { __m256 a_1 = _mm256_set1_ps(data1[u * n + j]); __m256 a_2 = _mm256_set1_ps(data1[u * n + j + 1 ]); __m256 a_3 = _mm256_set1_ps(data1[u * n + j + 2 ]); __m256 a_4 = _mm256_set1_ps(data1[u * n + j + 3 ]); __m256 a_5 = _mm256_set1_ps(data1[u * n + j + 4 ]); __m256 a_6 = _mm256_set1_ps(data1[u * n + j + 5 ]); __m256 a_7 = _mm256_set1_ps(data1[u * n + j + 6 ]); __m256 a_8 = _mm256_set1_ps(data1[u * n + j + 7 ]); __m256 b_1 = _mm256_loadu_ps(data2 + j * n + k); __m256 b_2 = _mm256_loadu_ps(data2 + (j + 1 ) * n + k); __m256 b_3 = _mm256_loadu_ps(data2 + (j + 2 ) * n + k); __m256 b_4 = _mm256_loadu_ps(data2 + (j + 3 ) * n + k); __m256 b_5 = _mm256_loadu_ps(data2 + (j + 4 ) * n + k); __m256 b_6 = _mm256_loadu_ps(data2 + (j + 5 ) * n + k); __m256 b_7 = _mm256_loadu_ps(data2 + (j + 6 ) * n + k); __m256 b_8 = _mm256_loadu_ps(data2 + (j + 7 ) * n + k); b_1 = _mm256_mul_ps(b_1, a_1); b_2 = _mm256_mul_ps(b_2, a_2); b_3 = _mm256_mul_ps(b_3, a_3); b_4 = _mm256_mul_ps(b_4, a_4); b_5 = _mm256_mul_ps(b_5, a_5); b_6 = _mm256_mul_ps(b_6, a_6); b_7 = _mm256_mul_ps(b_7, a_7); b_8 = _mm256_mul_ps(b_8, a_8); __m256 t_1 = _mm256_add_ps(b_1, b_2); __m256 t_2 = _mm256_add_ps(b_3, b_4); __m256 t_3 = _mm256_add_ps(b_5, b_6); __m256 t_4 = _mm256_add_ps(b_7, b_8); __m256 t_5 = _mm256_add_ps(t_1, t_2); __m256 t_6 = _mm256_add_ps(t_3, t_4); __m256 t_7 = _mm256_add_ps(t_5, t_6); __m256 t_c = _mm256_loadu_ps(data3 + u * n + k); __m256 t_8 = _mm256_add_ps(t_7, t_c); _mm256_storeu_ps(data3 + u * n + k, t_8); } } } } return true ; }
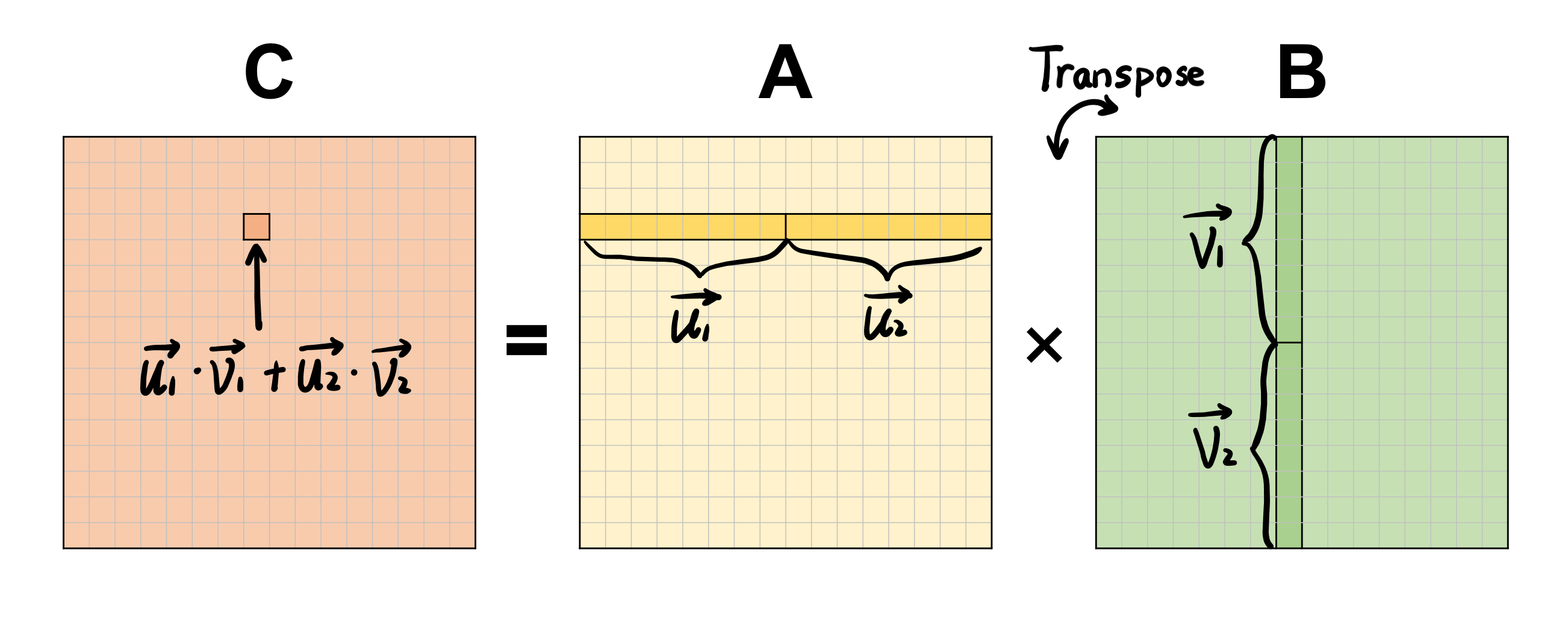
这是上述计算过程的图像解释,我们每次将$B$中的8个元素合并载入__mm256,再将$A$中的单个元素广播载入__mm256,二者批量相乘后再累加至对应8个元素中,通过u的循环就可以得到8×8分块的值。
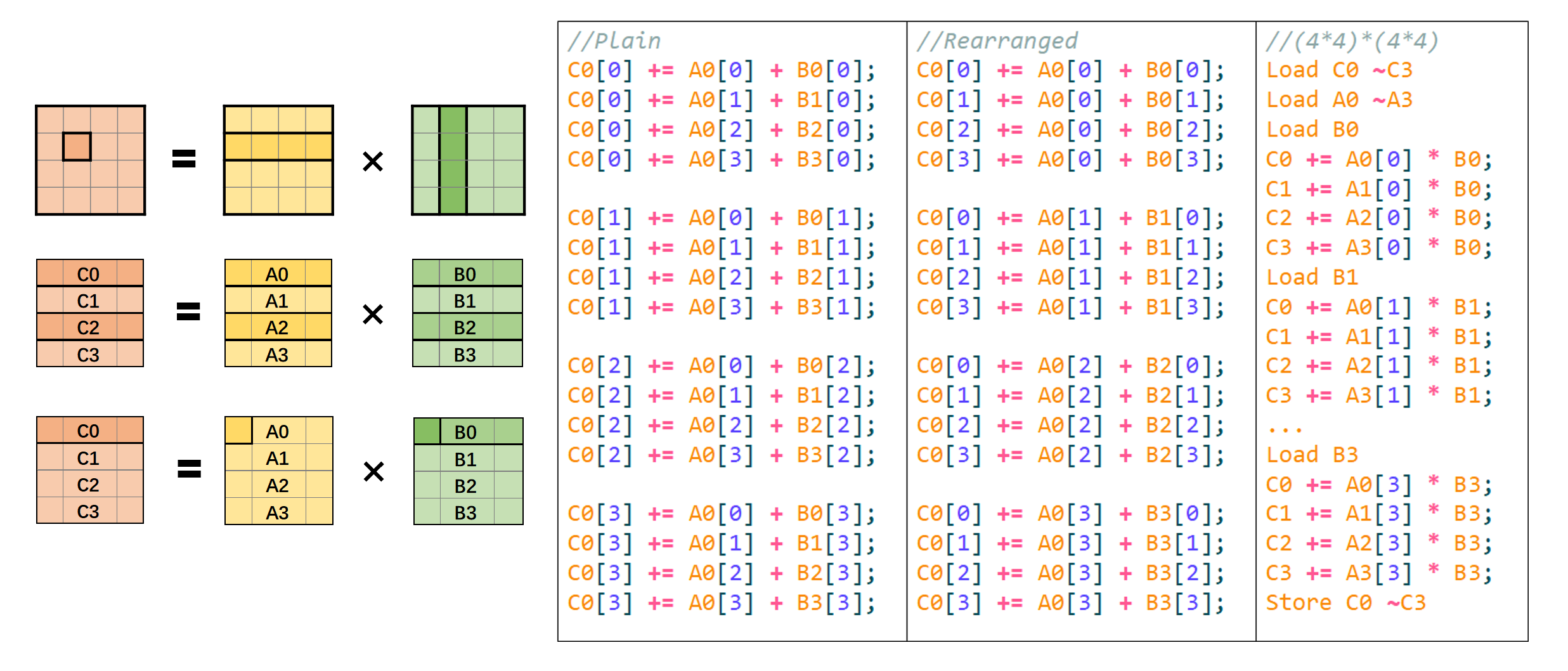
为了便于说明,我们以4×4的例子入手讲解,以下是计算C[0][0..3]的式子
1 2 3 4 C0[0 ]+=A0[0 ]+B0[0 ] C0[0 ]+=A0[1 ]+B1[0 ] C0[0 ]+=A0[2 ]+B2[0 ] C0[0 ]+=A0[3 ]+B3[0 ] C0[1 ]+=A0[0 ]+B0[1 ] C0[1 ]+=A0[1 ]+B1[1 ] C0[1 ]+=A0[2 ]+B2[1 ] C0[1 ]+=A0[3 ]+B3[1 ] C0[2 ]+=A0[0 ]+B0[2 ] C0[2 ]+=A0[1 ]+B1[2 ] C0[2 ]+=A0[2 ]+B2[2 ] C0[2 ]+=A0[3 ]+B3[2 ] C0[3 ]+=A0[0 ]+B0[3 ] C0[3 ]+=A0[1 ]+B1[3 ] C0[3 ]+=A0[2 ]+B2[3 ] C0[3 ]+=A0[3 ]+B3[3 ]
对于朴素乘法,我们对上述16个式子是“行优先”执行的,但如果按“列优先”的视角重排后,我们发现A可以一次性载入用作输出的计算,对于B则逐行拆分使用。利用AVX指令集,我们将四个元素的访存与计算向量化,则能达到提高效率的目的。
多线程 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 #include <pthread.h> struct PartialMatMulParams { size_t fromColumn, toColum, n; float *a, *b, *c; }; void *partialMatMul (void *params) struct PartialMatMulParams *p = (struct PartialMatMulParams *)params; size_t n = p->n; float *a = p->a; float *b = p->b; float *c = p->c; #pragma omp parallel for for (size_t i = p->fromColumn; i < p->toColum; i++) { for (size_t j = 0 ; j < n; j++) { for (size_t k = 0 ; k < n; k++) { c[j * n + i] += a[j * n + k] * b[k * n + i]; } } } return NULL ; } bool matmul_thread (Matrix *src1, Matrix *src2, Matrix *dst, size_t num_threads) if (!safe_check (src1, src2, dst)) { return false ; } register size_t n = src1->row; float *data1 = src1->data; float *data2 = src2->data; float *data3 = dst->data; pthread_t *threads = malloc (sizeof (pthread_t ) * num_threads); struct PartialMatMulParams *params = malloc (sizeof (struct PartialMatMulParams) * num_threads); for (size_t i = 0 ; i < num_threads; i++) { params[i].a = data1; params[i].b = data2; params[i].c = data3; params[i].n = n; params[i].fromColumn = i * (n / num_threads); params[i].toColum = (i + 1 ) * (n / num_threads); pthread_create (&threads[i], NULL , partialMatMul, ¶ms[i]); } for (size_t i = 0 ; i < num_threads; i++) { pthread_join (threads[i], NULL ); } free (threads); free (params); }
以上函数是笔者对于<pthread.h>库的实验品,在浅略阅读相关讲解与教程后所写,在实际运行测试中,虽然能正确得到结果,但以16线程运行的效率甚至低于无优化的朴素算法,且笔者对于该库的线程安全问题并不了解,因此仅作为学习过程的副产品,不参与后续效率比较。
Part 3 - Test & Comparison 测试说明 benchmark.c为本项目测试用代码,其中依次测试了矩阵乘法的各类实现的正确性与耗时。
矩阵尺寸由调试者输入,矩阵元素为随机生成的$[0,1]$的单精度浮点数。
乘法标准答案由cblas.h的cblas_sgemm()函数输出至矩阵$C$,其余函数输出至$D$并与之比较,会打印出首次误差情况。
考虑到使用了OpenMP提高效率,此处使用double omp_get_wtime()计算运行时间,单位为秒。
在运行一个函数前,程序会“预热”两次,即预先运行2次再计时。
下面是以matmul_avx_block8()为例的测试片段。
1 2 3 4 5 6 7 8 9 matmul_avx_block8 (A, B, D);matmul_avx_block8 (A, B, D);memset (D->data, 0 , sizeof (float ) * nn);time1 = omp_get_wtime (); matmul_avx_block8 (A, B, D);time2 = omp_get_wtime (); printf ("[AVX_block+OpenMP] %ld ms used\n" , (long int )(1000 * (time2 - time1)));printf (equals (C, D) ? "Result Accepted.\n" : "Wrong Result.\n" );memset (D->data, 0 , sizeof (float ) * nn);
x64平台测试结果 笔记本型号:Surface Pro7 孱弱的主动散热+外置风扇
系统:Linux version 5.10.16.3(WSL2),64位系统,基于x64处理器
处理器:Intel(R) Core(TM) i7-1065G7 CPU @ 1.30GHz 1.50 GHz
时间单位:毫秒(ms),0代表1ms内完成,/表示等待时间在作者的耐心之外(超过5分钟)
由于要预热,超出5分钟的函数笔者要等15分钟以上
Without addition compilation option
阶数/函数
plain
divide
plain+omp
avx_vec8
avx_block8
OpenBLAS
16
0
0
0
0
0
0
128
7
7
1
0
30
0
1024
3657
1366
792
194
257
7
2048
27677
11123
6783
1835
1496
43
4096
205834
116130
61203
12968
11397
395
8192
/
/
543397
124802
107255
2940
16384
/
/
/
/
/
24763
With -O2
阶数/函数
plain
divide
plain+omp
avx_vec8
avx_block8
OpenBLAS
16
0
0
0
0
0
0
128
2
0
0
0
28
0
1024
515
165
110
32
52
6
2048
4746
1727
933
623
232
46
4096
34098
15463
11363
5395
1765
395
8192
270939
139216
89797
46394
14359
3015
16384
/
/
/
/
196830^
24433
^: 在测试16384×16384矩阵的avx_block8函数时,即便笔者使用了外置散热手段,还是无法避免CPU长期高负荷计算过热导致的降频,因此该数据效率有明显下降。
With -O3
阶数/函数
plain
divide
plain+omp
avx_vec8
avx_block8
OpenBLAS
16
0
0
0
0
6
0
128
0
0
0
115
59
2
1024
134
131
47
112
89
7
2048
1648
975
357
607
299
48
4096
13601
7905
3099
5386
1837
388
8192
112437
74809
41208
44041
14188
3069
16384
/
/
/
/
188428^
24325
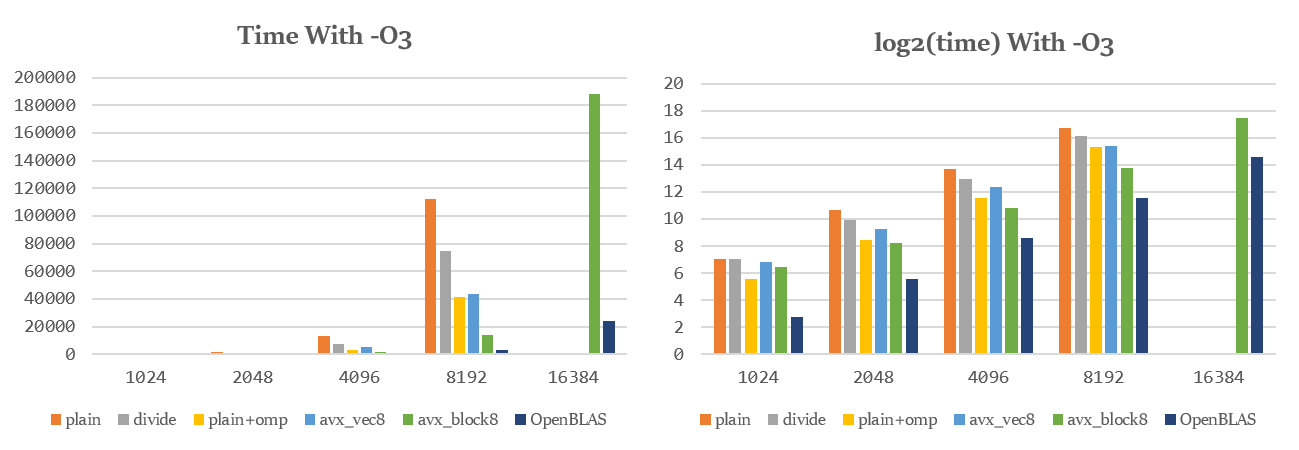
笔者将电脑关闭冷却后,使用-O3编译,发现如下现象:
对于阶数在2048以下的矩阵,自行实现的SIMD优化函数效率有所下降,而对于较大矩阵,自行实现的SIMD优化函数效率基本不变。
未引入手动SIMD优化的函数效率有较大提高,但在大规模计算时效率低于SIMD优化
又降频了,说明效率门槛从访存速度转移至算力。
随后尝试了-Ofast编译,效果在误差允许范围内与-O3几乎相同。
经过查询
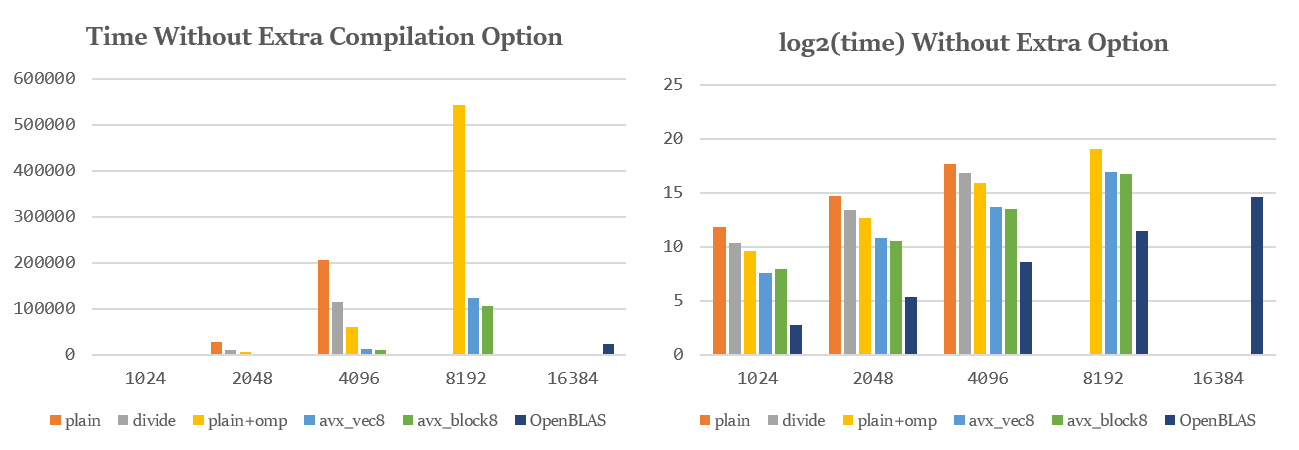
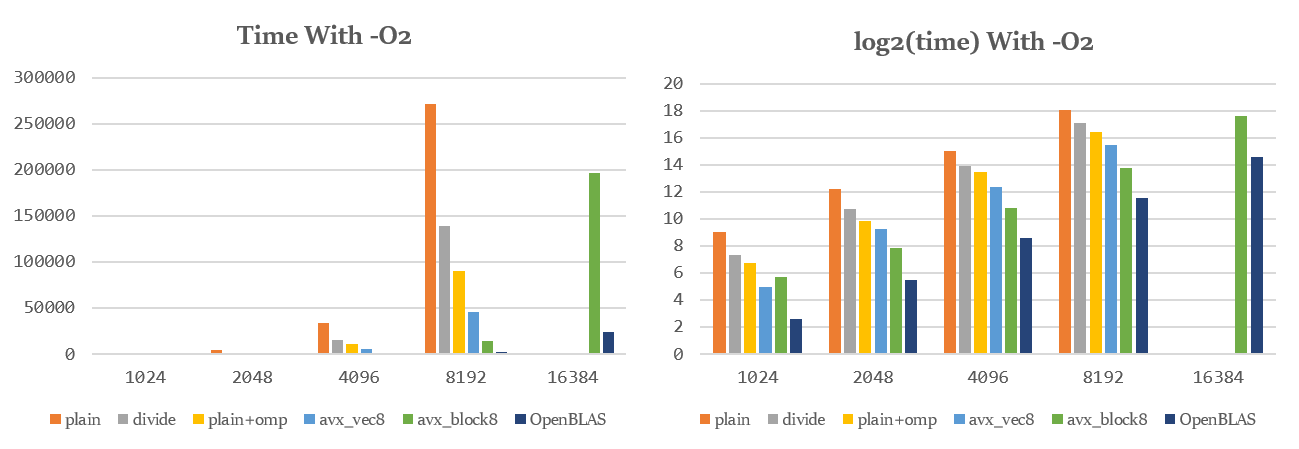
图表比较 下图是矩阵乘法的不同实现对于各规模矩阵的用时柱状图,单位ms,超时部分未画出。
为了方便观察比较,此处对时间取log2对数,得到右侧各图。
自行实现的各算法中,开启-O2时耗时比约为:
由上述原因,只看n=16384时,自行实现的最快算法avx_block8耗时也达到了OpenBLAS的8倍左右,但在其他规模下,avx__block8可以达到OpenBLAS的4~5倍。
由右侧各图可以观察到,在开启-O2编译后,avx_block8的log2(time)与OpenBLAS相差只有2左右,即达到了约1/4的效率。
ARM平台测试结果 除在本机运行外,笔者在EAIDK310开发板上运行了基于<arm_neon.h>的版本。
开发板运行内存1GB,内置存储8GB。
CPU为ARM 4核 64位处理器,四核Cortex-A53,最高1.3GHz。
理论上,开发板可以为16k×16k的矩阵分配空间,但实际运行时,进程则被系统killed掉了,说明EAIDK310可能实际上无法支持申请这么大的空间。同时,由于更大规模的矩阵乘法运行时间过长,此处仅测试了16~4096规模的矩阵。
Without addition compilation option
阶数/函数
plain
divide
plain+omp
neon_vec4
neon_block4
OpenBLAS
16
0
0
0
0
1
0
128
87
48
31
44
48
0
1024
44629
20449
11230
4749
5536
156
2048
/
/
89900
30015
59238
1226
4096
/
/
/
/
/
9659
With -O2
阶数/函数
plain
divide
plain+omp
neon_vec4
neon_block4
OpenBLAS
16
0
0
0
0
2
0
128
20
9
5
76
11
0
1024
10283
3930
2611
1196
1473
167
2048
82239
32929
20859
9483
30989
1228
4096
/
/
169994
75110
/
9670
With -O3
阶数/函数
plain
divide
plain+omp
neon_vec4
neon_block4
OpenBLAS
16
0
0
0
0
3
0
128
6
2
1
75
12
0
1024
3021
1781
893
1221
1098
159
2048
24062
16943
7828
9495
34779
1223
4096
/
136914
82110
74115
/
10050
让人比较郁闷的是NEON仅有4个一组绑定的float,而没有__mm256的代替品,因此笔者将分块步长从8变成4,牺牲了效率,分块效率变得不如向量化效率,可能也有开发板算力弱于电脑的原因。上述三种编译下的耗时比例关系与上文类似,故此不做赘述。
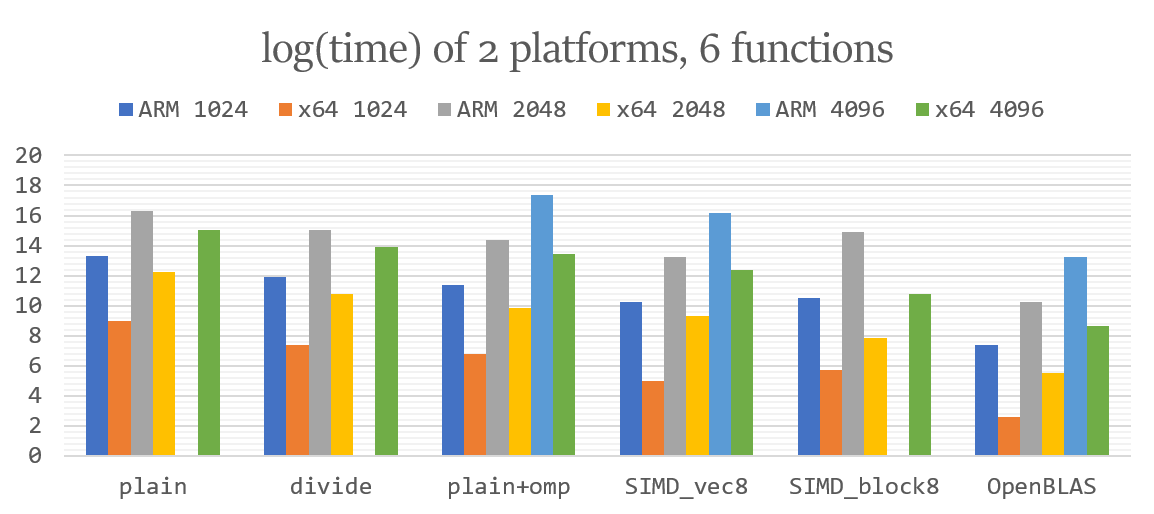
跨平台的比较 本项目分别在x64和ARM架构的平台进行了测试,从结果可以大致算出x64平台的效率大约是ARM平台的16倍,在下图中表现为:相同算法下左柱(ARM)比相邻的右柱(x64)高出大约4。
随着矩阵阶数的按2倍乘,各算法耗时也大致呈8倍增长,符合$O(N^3)$算法的特征,由此可见,OpenBLAS底层似乎也采用的是$O(N^3)$的算法,但对许多细节进行了展开和优化来降低常数。
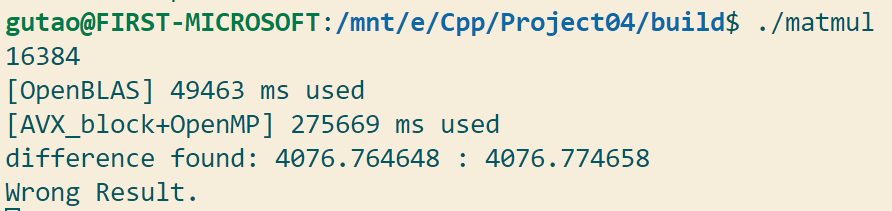
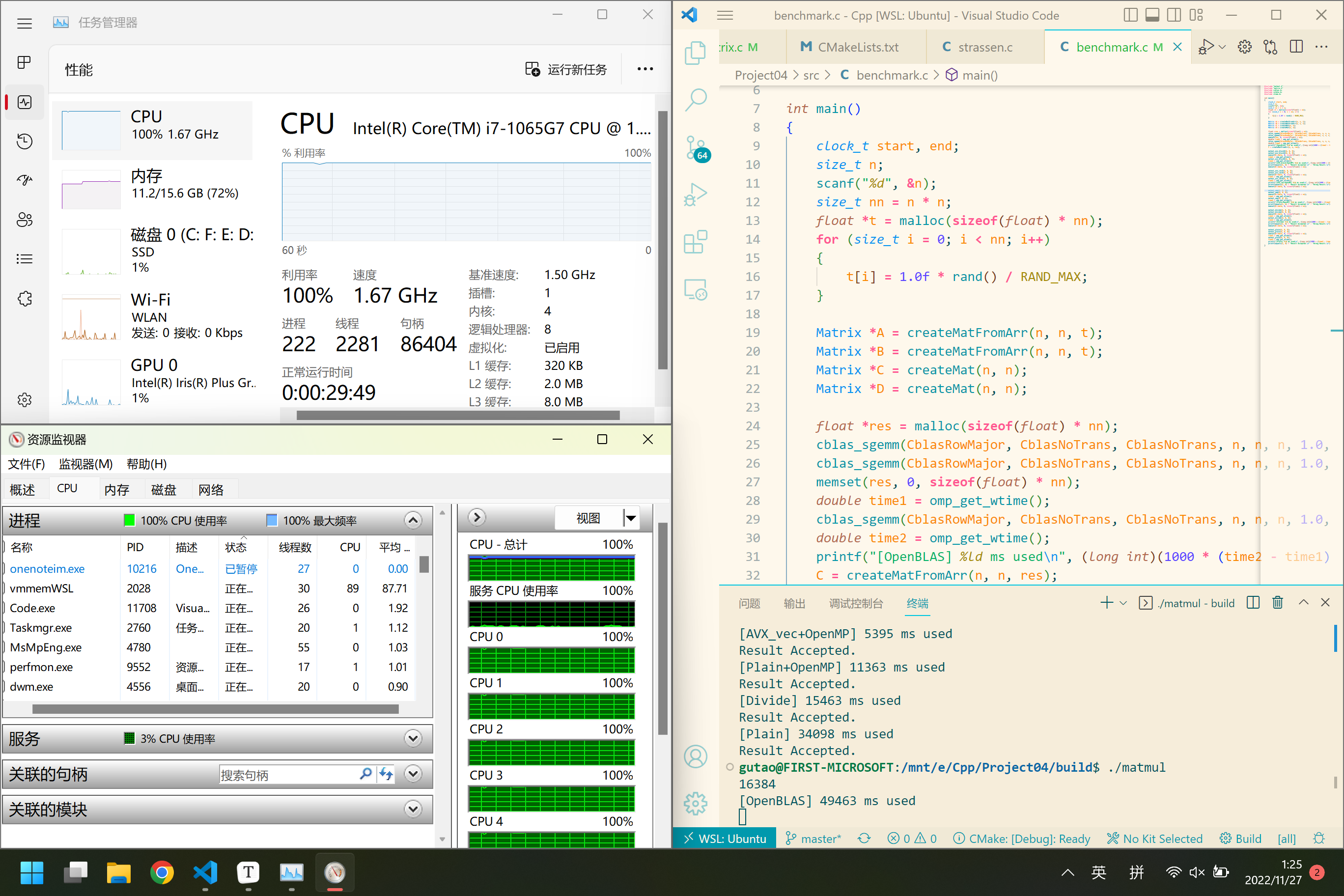
Part 4 - Difficulties & Solutions Difficulty I. 误差处理 笔者在测试时发现,对于规模在2048以上的矩阵乘法,很容易产生0.001的误差,(通常是OpenBLAS与自己实现的不同,而自己实现的几个往往成对相同)。下图是某个凌晨一点钟,没开风扇降频跑16k规模矩阵时得到的结果。
Solution 经同学提醒,可以将误差设置为数据的1‰而非0.001,这样的误差要求对于进行了很多次加、乘法得到的结果也都是可以接受的。
不过为了比较时的效率,benchmark.c依然采用旧版比较,适当放宽误差到0.01时可以验证乘法的正确性,既然保证了正确性,精确到哪一位才算正确似乎也没有那么重要了。
1 2 3 #define float_equal(x, y) ((x - y) < 1e-3 && (y - x) < 1e-3) #define mx(x, y) ((x) > (y) ? (x) : (y)) #define float_equal2(x, y) (x > y ? (x - y < mx(x, 1) * 1e-3) : (y - x < mx(y, 1) * 1e-3))
Difficulty II. Strassen 与同学讨论的过程中,笔者了解到$O(N^{lg7})≈O(N^{2.81})$复杂度的Strassen算法,并且尝试自己写了一下,通过了正确性测试,但效率非常悲观,仅比朴素略快一筹。
Solution 随后笔者分析了原因:Strassen算法将矩阵运算中的8次子矩阵乘法与4次子矩阵加法,分别变为了7次和18次,即以额外的14次加法为代价减少一次乘法,在阶数很高时才能体现差距,且笔者在实现Strassen时并未使用SIMD进行加速,导致加法运算并未得到很好的优化,而分治的截取、合并等操作导致内存访问的跳跃数较高,虽然从软件层面降低了复杂度,但在硬件层面增大了操作复杂性。
另外,该算法的优化幅度为$O(N^{0.19})$,而当$N=16384$时,也只有理论上限6.32倍的提升,矩阵规模越小优化越不明显。加上访问不连续、矩阵分块等操作带来的额外复杂度,总体呈现负优化。也许加上合适的SIMD优化能提高其效率。
Difficulty III. Segmentation Fault SIMD优化过程中屡次出现段错误,笔者试图使用memalign函数在创建矩阵时将data对齐,粒度设置为32,以便后续的load等操作,但发现写入数据时会导致段错误。
Solution 查询memalign的用法后发现并无异常,但就是无法对申请的内存进行正常读写,于是笔者推测可能是申请的空间过大,无法通过该函数申请到一块连续、对齐的内存用于存储数据,导致并未将data指向一段合法内存,因此读写时会段错误。考虑到申请如此大块的内存的确不太现实,笔者选择在载入时牺牲一定效率,换用loadu_ps来对未对齐的数据进行载入,效率还算不错,借此实现了本项目最快的函数,对齐后也许还能更快。
Difficulty IV. 64k×64k 一个float四字节,$64k×64k=2^{32}=4,294,967,296$个元素,也就是对于仅一个64k阶矩阵,就要为data指针分配$2^{32}×4/1024^3=16GB$内存,实在是有点难为渣机了。而对于运行内存1GB,内置存储8GB的EAIDK310而言,条件会更加苛刻。
Solution 办法总比问题多,但效果不一定好。对于如此巨大的矩阵,我们可以将其写入文件,在访问某块元素时再读取载入进行运算,运算后写回文件。笔者不得不承认这是一个办法,但对于能存下的矩阵,运算耗时也已经到了难以等待的程度,如果在每次读写元素时再加上文件操作时间,恐怕要等到天荒地老、海枯石烂了,因此虽然能这样解决,但并没有必要。
Part 5 - Summary & Blooper 首先,感谢您能读到这里,该部分是对项目开发过程的总结与花絮的分享。
本项目在尝试了若干种优化方法后,结合OpenMP、SIMD和分块等方法对矩阵乘法进行了不同程度的优化,将耗时门槛从访存转移到了计算,效率达到了OpenBLAS的1/4左右。
由于笔者的电脑只有一块Intel Iris Plus Graphics核显,且本次项目的大致重心在于如何最大限度利用CPU进行矩阵乘法的运算,笔者几乎用尽解数才写出了本项目最快的函数,然而与OpenBLAS依然相差甚远,大约可以理解于老师当年与完备的库相比时感受到的“绝望”的感觉了。不过想想那个项目无论从开发周期还是开发团队都远超这个用时二十余小时的单人项目,内心倒也释然许多。
11.27凌晨一点,笔者在测试16k矩阵乘法时,CPU八核顶着高温降频运转,为了等待自己最快的一个函数的运行结果,守在电脑前近二十分钟(预热两次真的很慢),得到了下面的结果:
本来已经完全不抱希望了,但就在快要没耐心的时候程序给出了答案,虽然有一点误差,但当时还是挺感动的。然而第二天在加上外置风扇、酒精喷雾等外置散热的帮助下,效率得到了很大的提升,令人感慨好硬件的重要性。
本次项目兼具技术性和挑战性,还是非常有趣的,也让人深刻意识到自己和行业标准的差距,此后这门课仅剩一次project,且做且珍惜啦。