Cuckoo!
0%

CS217 数据结构与算法分析 期末复习

Posted on In
复习再多，考试想不出来就是想不出来(。_。;)

Algorithm visualization

Introduction

Incremental technique, Recursive technique

Divide-and-conquer Strategy

Iteration, Recursion

Algorithm Analysis

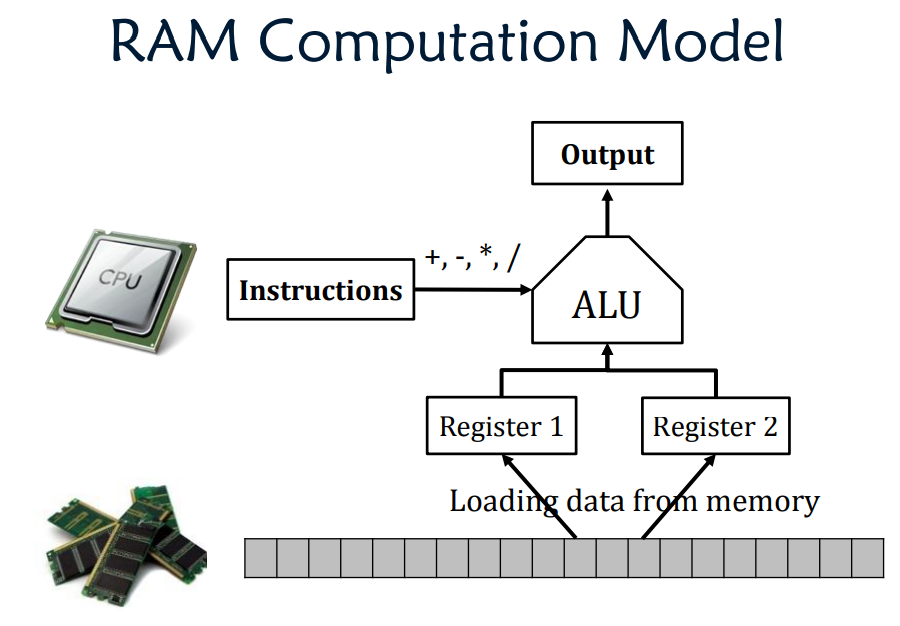
image.png

CPU Basic (atomic) operations

  • Initialization
  • Arithmetic
  • Comparison / Branching
  • Memory Access

Cost analysis, Correctness analysis

Pseudocode

Binary Search Algorithm

1
2
3
4
5
6
7
8
9
10
11
//end state: l>r, answer registered as ans
while (l<=r)
{
    int mid=(l+r)/2;
    if (check(mid))
    {
        ans=mid;
        r=mid-1;
    }
    else l=mid+1;
}printf("%d",ans);
1
2
3
4
5
6
7
//end state: l==r, answer=l=r
while (l<r)
{
    int mid=(l+r)/2;
    if (check(mid)) r=mid
    else l=mid+1;
}printf("%d",l); 
1
2
3
4
5
6
7
8
//The smallest element no less than key
int l=1,r=n;while (l<r)
{
    int mid=(l+r)/2;
    if (a[mid]>=key) r=mid; 
    else l=mid+1;
}
return l;
1
2
3
4
5
6
7
8
//The greatest element no greater than key
int l=1,r=n;while (l<r)
{
    int mid=(l+r+1)/2;
    if (a[mid]<=key) l=mid; 
    else r=mid-1;
}
return l;

Big-O Notation

image.png

Big-Ω Notation

image.png

Big-Θ Notation

image.png

Sorting

Selection sort

image.png

Insertion sort

image.png

Bubble sort

image.png

Merge sort

image.png

image.png

Matser Theorem

image.png

Quick sort

Worst $O(n^2)$, Expected $O(n\log n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function quickSort(arr, left, right) {
    var len = arr.length,
        partitionIndex,
        left = typeof left != 'number' ? 0 : left,
        right = typeof right != 'number' ? len - 1 : right;

    if (left < right) {
        partitionIndex = partition(arr, left, right);
        quickSort(arr, left, partitionIndex-1);
        quickSort(arr, partitionIndex+1, right);
    }
    return arr;
}

function partition(arr, left ,right) {     // 分区操作
    var pivot = left,                      // 设定基准值（pivot）
        index = pivot + 1;
    for (var i = index; i <= right; i++) {
        if (arr[i] < arr[pivot]) {
            swap(arr, i, index);
            index++;
        }        
    }
    swap(arr, pivot, index - 1);
    return index-1;
}
//javascript version from runoob.com

$e_i$ and $e_j$ are compared IFF either one is the first among $e_i, e_{i+1},\cdots, e_j$ picked as a pivot.

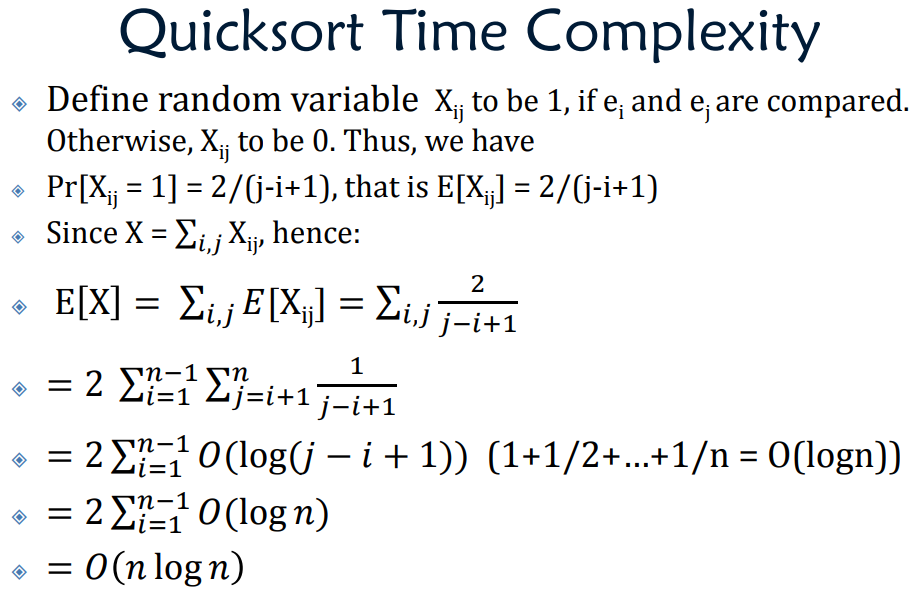
image.png

Complexity Summary

Sort Average Time Complexity Space Complexity
Selection $O(n^2)$ $O(1)$
Insertion $O(n^2)$ $O(1)$
Bubble $O(n^2)$ $O(1)$
Heap $O(n\log n)$ $O(1)$
Merge $O(n\log n)$ Depends
Quick $O(n\log n)$ $O(1)$

Shell sort

1
2
3
4
5
6
7
8
9
10
11
void shell_sort(int arr[], int len) {
        int gap, i, j;
        int temp;
        for (gap = len >> 1; gap > 0; gap >>= 1)
                for (i = gap; i < len; i++) {
                        temp = arr[i];
                        for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
                                arr[j + gap] = arr[j];
                        arr[j + gap] = temp;
                }
}

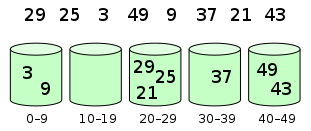
Counting sort

Radix sort

Bucket sort

Linked List

Operation Time Complexity Space Complexity
Insert $O(n)$ $O(1)$
Delete $O(n)$ $O(1)$
Find $O(n)$ $O(1)$
Update $O(n)$ $O(1)$

Double linked list

Circular linked list

Stack & Queue

Stack

First In Last Out

image.png

Applications: Delimiters balance problem, Evaluating arithmetic expressions, The runtime stack in memory

Prefix/Infix/Postfix expression

Queue

First In First Out

image.png

Ring queue

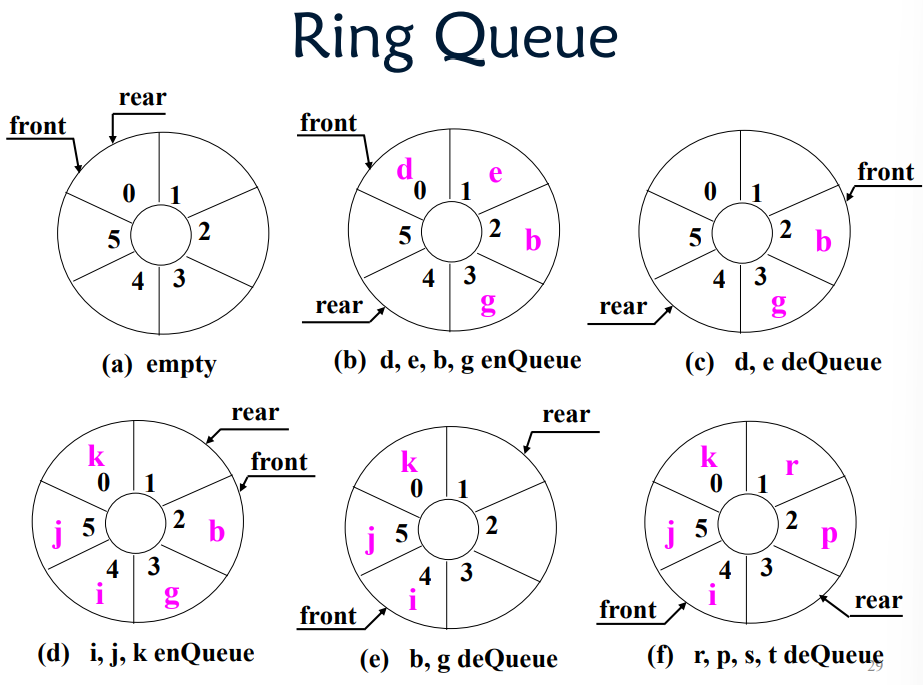
image.png

All operations above takes $O(1)$ time complexity.

String

String matching

Brute Force $O(mn)$

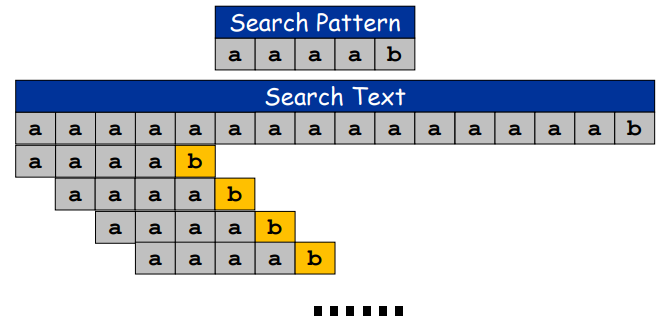
image.png

Rabin-Karp Algorithm $O(mn)$

image.png

KMP $O(m+n)$

image.png

image.png

FSA

  • $Q$, a set of states
  • $q_0\in Q$, the start state
  • $A\subseteq Q$, the accepting states
  • $\Sigma$, the input alphabet
  • $\delta$, the transition function $Q\times \Sigma→Q$

image.png

Tree

Internal nodes, leaf nodes, root

(proper) ancestor, descendant

Path, Depth, Level, Height

(full, complete) k-ary tree

preorder, inorder, postorder traversal

Character Encoding & Huffman Tree

image.png

Given a Huffman tree, it includes at least 2 nodes, assume node $u$ and node $v$ have the top-2 lowest frequencies, then

  1. node $u$ and $v$ have the same parent node
  2. $depth(u)$ and $depth(v) \ge depth(x)$, where node $x$ is any leaf node in the Huffman tree.

Huffman encoding is the optimum prefix code, i.e., the space cost is minimized.Proof

  1. A tree with $n$ nodes with $n-1$ edges
  • For each non-root node v, it has one and only one edge point to itself.
  • A tree with n nodes, thus the number of non-root nodes is n-1.
  • Thus, this tree has n-1 edges.
  1. Let $T$ be a tree where every internal node has at least 2 child nodes. If $m$ is the number of leaf nodes, then the number of internal nodes is at most $m-1$.
  • Suppose internal node $v$ has $x_v$ child nodes
  • The average child nodes of each internal node is $x$
  • It has $m$ leaf nodes, thus it has $m/x$ parent nodes at most, i.e., they are parent of leaf nodes.
  • For $m/x$ internal nodes, it has at most $m/x^2$ parents.
  • For $m/x^2$ internal nodes, it has at most $m/x^3$ parents.
  • …
  • The total number of internal nodes is $m/x + m/x^2 + … + 1$
  • It is at most m-1.
  1. A complete binary tree with $n ≥ 2$ nodes has height $O(\log n)$
  • Suppose the height is $h$.
  • The number of nodes at each level:
  • Level 0: $2^0 = 1$, Level 1: $2^1 = 2 $
  • Level 2: $2^2 = 4$, Level 3: $2^3 = 8$
  • …
  • Level $h-1$: $2^(h-1)$, Level $h$: $x (x \ge 1) $
  • Thus, $2^0 + 2^1 + … 2^{h-1} + x = n$
  • $(1-2^{h-1})/(1-2) = n-x → 2^{h-1} < n $
  • Thus, $h = O(\log n)$

Advanced Binary Trees

Heap

  • Complete binary tree
  • $O(n)$ space consumption
  • $O(\log n)$ insertion time
  • $O(\log n)$ delete-min time

Suppose that node $u$ of $T$ is stored at $A[i]$. Then, the left child of $u$ is stored at $A[2i]$, and the right child at $A[2i+1]$.

Suppose that node $u$ of $T$ is stored at $A[i]$. Then, the parent of $u$ is stored at $A[ \left \lfloor i/2 \right \rfloor ]$.

Root-fix operation: Build a heap with $O(n)$ time.

$O(\sum\limits_{i=0}^{h-1}(h-i)\times2^i)=O(2^h)=O(n)$

Binary Search Tree

predecessor($\max\{a[i]\le q\}$), successor($\min\{a[i]\ge q\}$): $O(h)$

↙↘↘↘↘↘，↘↙↙↙↙↙

Insert: $O(h)$

image.png

Delete: $O(h)$

image.png

BBST

For every internal node $u$ of $T$, the height of the left subtree of $u$ differs from that the right subtree of $u$ by at most 1.

Proof: A balanced binary tree with $n$ nodes has height $O(\log n)$.

To construct a BBST with greatest height using $n$ nodes, each internal node should has subtrees that differ 1 in height. Denote $f(h)$ as the least number of nodes of a BBST with height $h$, then

$f(1)=1, f(2)=2$

$f(h)=f(h-1)+f(h-2)+1$

$f(h)+1=f(h-1)+1+f(h-2)+1$

$f(h)=\frac{1}{\sqrt 5}[(\frac{1+\sqrt 5}{2})^{h+1}-(\frac{1-\sqrt 5}{2})^{h+1}]-1$

$n\ge \frac{1}{\sqrt 5}[(\frac{1+\sqrt 5}{2})^{h+1}-(\frac{1-\sqrt 5}{2})^{h+1}]-1$

$h\le c\log n, h=O(\log n)$

Insertion time analysis?

Deletion time analysis?

Graph

BFS

BFS tree, SSSP

DFS

DFS tree, Cycle detection, topological sort

Parenthesis Theorem: all the following are true:

  • If $u$ is a proper ancestor of $v$ in DFS-tree of $T$, then $I(u)$ contains $I(v)$.
  • If $u$ is a proper descendant of $v$ in DFS-tree of T, then $I(u)$ is contained in $I(v)$ .
  • Otherwise, $I(u)$ and $I(v)$ are disjoint.

White Path Theorem: let $u$ be a vertex in $G$. Consider the moment when $u$ is pushed into the stack in the DFS algorithm. Then a vertex $v$ becomes a proper descendant of $u$ in the DFS-forest IFF we can go from $u$ to $v$ by travelling only on white vertices.

Cycle Theorem: let $T$ be an arbitrary DFS-forest. $G$ contains a cycle if and only if there is a backward edge with respect to $T$.

  • If: trivial
  • only if: Suppose the cycle is $v_1 → 𝑣_2 → ⋯ → 𝑣_𝑘 → 𝑣_1$, let $𝑣_𝑖$ be the first to enter the stack. Then by white path theorem, all the other vertices in the cycle must be proper descendants of $𝑣_𝑖$ in the DFS-forest. This means the edge pointing to $𝑣_𝑖$ in the cycle is a backward edge.

Dijkstra: $O((|V|+|E|)\log |V|)$

image.png

Correctness proof:

image.png

Minimum Spanning Tree (Prim): $O(|V|\log |V|+|E|)$

image.png

Strongly Connected Components $O(|V|+|E|)$

  1. obtain $G^R$

  2. DFS on $G^R$, obtain $L^R$

  3. obtain $L$ by reversing $L^R$
  4. DFS on $G$ according to $L$
  5. obtain SCC from DFS-forest

Correctness proof:

  1. Obtain $G^{SCC}$ by shrinking nodes

  2. sink SCC: SCC without in-degree

  3. DFS on $G$ starting from vertices of sink SCC.

Let $S_1$ , $S_2$ be SCCs such that there is a path from $S_1$ to $S_2$ in $G^SCC$. In the ordering of $L$, the earliest vertex in $S_2$ must come before the earliest vertex in $S_1$