Outline
- Counting
- Relation
- Graphs
- Tree
- P, NP and NPC Problems
Chapter 11 - Counting
Basic Counting Rules: the Product Rule & the Sum Rule
Pigeonhole Principle:
If there are more objects than bins then there is at least one bin with more than one object.
Generalized Pigeonhole Principle:
If $N$ objects are placed into $k$ bins, then there is at least one bin containing at least $⌈N/k⌉$ objects.
Inclusion-Exclusion Principle:
$|A\cup B|=|A|+|B|-|A\cap B|$
$|\bigcup\limits_{i=1}^{n}E_i|=\sum\limits_{k=1}^{n}(-1)^{k+1}\sum\limits_{1\le i_1<i_2<\cdots<i_k\le n}|E_{i_1}\cap E_{i_2}\cap\cdots \cap E_{i_k}|$
Permutations:
$P(n,k)=\frac{n!}{(n-k)!}$
Binomial Coefficient:
$\left(\begin{array}{c}
n \\
k
\end{array}\right)=C(n, k)=\frac{n!}{k!(n-k)!}$
Some Properties of Binomial Coefficients:
$\left(\begin{array}{c}
n \\
k
\end{array}\right)=\left(\begin{array}{c}
n \\
n-k
\end{array}\right)$
$\sum\limits_{i=0}^{n}\left(\begin{array}{c}
n \\
i
\end{array}\right)=2^n$
Pascal identity:
$\left(\begin{array}{c}
n \\
k
\end{array}\right)=\left(\begin{array}{c}
n-1 \\
k-1
\end{array}\right)+\left(\begin{array}{c}
n-1 \\
k
\end{array}\right)$
Pascal’s Triangle:
$\begin{array}{l}
1 \\
1 \quad 1 \\
\begin{array}{lll}
1 & 2 & 1
\end{array} \\
\begin{array}{llll}
1 & 3 & 3 & 1
\end{array} \\
\begin{array}{lllll}
1 & 4 & 6 & 4 & 1
\end{array} \\
\begin{array}{llllll}
1 & 5 & 10 & 10 & 5 & 1
\end{array} \\
\begin{array}{lllllll}
1 & 6 & 15 & 20 & 15 & 6 & 1
\end{array} \\
\end{array}$
The Binomial Theorem:
$(x+y)^n=\sum\limits_{i=0}^{n}\left(\begin{array}{c}
n \\
i
\end{array}\right)x^{n-i}y^i$.
Trinomial Coefficients:
When $k_1+k_2+k_3=n$
$\left(\begin{array}{ccc}
& n & \\
k_{1} & k_{2} & k_{3}
\end{array}\right)=\frac{n!}{k_1!k_2!k_3!}$
The Polynomial Theorem:
$(a_1+a_2+\cdots+a_m)^n=\sum\limits_{x_1+x_2+\cdots+x_m=n}\frac{n!}{x_1!x_2!\cdots x_m!}a_1^{x_1}a_2^{x_2}\cdots a_m^{x_m}$
Solving Linear Recurrence Relations of degree 2:
$a_n=c_1a_{n-1}+c_2a_{n-2}$
characteristic equation: $r^2-c_1r-c_2=0$
If CE has 2 distinct roots $r_1\ne r_2$, the solution: $a_n=\alpha_1r_1^n+\alpha_2r_2^n$
Solving Linear Recurrence Relations of degree k:
$a_n=\sum\limits_{i=1}^kc_ia_{n-i}$
CE: $r^k-\sum\limits_{i=1}^k c_ir^{k-i}=0$
If CE has $k$ distinct roots $r_i$, then the solution: $a_n=\sum\limits_{i=1}^k \alpha_ir_i^n$
The Case of Degenerate Roots in General:
Suppose there are $t$ roots $r_1,\cdots, r_t$ with multiplicities $m_1,\cdots,m_t$. Then the solution:
Linear Nonhomogeneous Recurrence Relations:
$a_n=F(n)+\sum\limits_{i=1}^kc_ia_{n-i}$
- Solve $a_n=\sum\limits_{i=1}^kc_ia_{n-i}$ and get $a_n=h(n)$
- Solve particular solution $p(n)$
- $a_n=p(n)+h(n)$
Generating Functions:
$G(x)=a_0+a_1x+\cdots+a_kx^k+\cdots=\sum\limits_{k=0}^{\infty}a_kx^k$
Examples of Generating Functions:
$G(x)=1/(1-x)$ for $|x|<1$
$1,1,1,1,1,\cdots$
$G(x)=1/(1-ax)$ for $|ax|<1$
$1,a,a^2,a^3,a^4,\cdots$
$G(x)=1/(1-x)^2$ for $|x|<1$
$1,2,3,4,5,\cdots$
$G(x)=1/(1-ax)^2$ for $|ax|<1$
$1,2a,3a^2,4a^3,5a^4,\cdots$
Operations of Generating Functions:
Let $f(x)=\sum\limits_{k=0}^{\infty}a_kx^k$, and $g(x)=\sum\limits_{k=0}^{\infty}b_kx^k$
Then
Convolution Rule:
Let $A(x)$ be the generating function for selecting items from a set $A$, and let $B(x)$ be the generating function for selecting items from a set $B$ disjoint from $A$. Then the generating function for selecting items from the union $A ∪ B$ is the product $A(x) \cdot B(x)$.
e.g. Number of ways to select $n$ balls with $k$ colors.
$D(x)=1/(1-x)^k$, $d_n=[x^n] (1/(1-x)^k)=\left(\begin{array}{c}n+k-1 \\n\end{array}\right)$
Useful Generating Functions:
$\begin{aligned}
(1+x)^{n} & = \sum_{k=0}^{n} C(n, k) x^{k} \\
(1+a x)^{n} & = \sum\limits_{k=0}^{n} C(n, k) a^{k} x^{k} \\
\left(1+x^{r}\right)^{n} & = \sum\limits_{k=0}^{n} C(n, k) x^{r k} \\
\frac{1-x^{n+1}}{1-x} & = \sum\limits_{k=0}^{n} x^{k} = 1+x+x^{2}+\cdots+x^{n} \\
\frac{1}{1-x} & = \sum\limits_{k=0}^{\infty} x^{k} = 1+x+x^{2}+\cdots \\
\frac{1}{1-a x} & = \sum\limits_{k=0}^{\infty} a^{k} x^{k} = 1+a x+a^{2} x^{2}+\cdots \\
\frac{1}{1-x^{r}} & = \sum\limits_{k=0}^{\infty} x^{r k} = 1+x^{r}+x^{2 r}+\cdots \\
\frac{1}{(1-x)^{2}} & = \sum\limits_{k=0}^{\infty}(k+1) x^{k} = 1+2 x+3 x^{2}+\cdots \\
\frac{1}{(1-x)^{n}} & = \sum\limits_{k=0}^{\infty} C(n+k-1, k) x^{k} \\
\frac{1}{(1+x)^{n}} & = \sum\limits_{k=0}^{\infty} C(n+k-1, k)(-1)^{k} x^{k} \\
\frac{1}{(1-a x)^{n}} & = \sum\limits_{k=0}^{\infty} C(n+k-1, k) a^{k} x^{k} \\
e^{x} & = \sum\limits_{k=0}^{\infty} \frac{x^{k}}{k !} = 1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\cdots \\
\ln (1+x) & = \sum\limits_{k=0}^{\infty} \frac{(-1)^{k+1} x^{k}}{k} = x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+\cdots
\end{aligned}$
r-Combinations from a Set:
An n-combination with repetition allowed, or a multiset of size $n$, chosen from a set of $k$ elements, is an unordered selection of elements with repetition allowed.
number of n-combinations: $C(n+k-1,n)$
Chapter 12 - Relation
Properties of Relations:
Reflexive Relation:$\forall a\in A$, $(a,a)\in R$
Irreflexive Relation:$\forall a\in A$, $(a,a)\notin R$
- Symmetric Relation:$\forall a,b\in A$, $(a,b)\in R→(b,a)\in R$
Antisymmetric Relation:$\forall a,b\in A$, $(a,b)\in R\wedge (b,a)\in R→a=b$
Transitive Relation:$\forall a,b,c\in A$, $(a,b)\in R\wedge (b,c)\in R→(a,c)\in R$
Combining Relations:
Using set operations.
Composite of Relations:
$(a,b)\in R$, $(b,c)\in S$, then $(a,c)\in S\circ R$
The powers $R^n$, for $n=1,2,3,\cdots$, is defined inductively by
$R^1=R$ and $R^{n+1}=R^n\circ R$
The relation $R$ on a set $A$ is transitive IFF $R^n\subseteq R$ for $n=1,2,3,\cdots$
Number of Reflexive Relations:
The number of reflexive relations on a set $A$ with $|A|=n$ is $2^{n(n-1)}$
Proof: $n$ diagonal elements fixed, the other $n(n-1)$ elements are free to choose.
Representing Relations:
explicit list/table, function $f:D→\{T,F\}$, 01 matrix, directed graph…
Closures of Relations:
Let $R$ be a relation on a set $A$. A relation $S$ on $A$ with property $P$ is called the closure of $R$ with respect to $P$ if $S$ is subset of every relation $Q$ ($S\subseteq Q$) with property $P$ that contains $R$ ($R\subseteq Q$).
$S$ is the minimal set containing $R$ satisfying the property $P$.
- reflexive closures
- symmetric closures
- transitive closures
Path Length:
Let $R$ be relation on a set $A$. There is a path of length $n$ from $a$ to $b$ IFF $(a,b)\in R^n$.
Proof by induction.
Let $A$ be a set with $n$ elements, and $R$ a relation on $A$. If there exists a path from $a$ to $b$ with $a\ne b$, then there exists a path of length $\le n-1$.
Connectivity Relation:
Let $R$ be a relation on a set $A$. The connectivity relation $R^\star$ consists of all pairs $(a,b)$ such that there is a path (of any length) between $a$ and $b$ in $R$.
The transitive closure of a relation $R$ equals the connectivity relation $R^\star$.
Proof:
$R^\star$ is transitive.
$(a,b)\in R^\star$ and $(b,c)\in R^\star$, then there are paths from $a$ to $b$ and from $b$ to $c$ in $R$. Thus, there is a path from $a$ to $c$ in $R$. This means that $(a,c)\in R^\star$.
$R^\star\subseteq S$ whenever $S$ is a transitive relation containing $R$.
Suppose that $S$ is a transitive relation containing $R$.
Then $S^n$ is also transitive and $S^n\subseteq S$.
We have $S^\star\subseteq S$. Thus $R^\star\subseteq S^\star\subseteq S$.
Transitive Closure Algorithm:
Roy-Warshall Algorithm ($\Theta(n^3)$)
1 | // computes R* ith zero-one matrices |
n-ary Relations & Relational Databases:
domains, degree, functional, primary key, composite key, selection, projection, join…
Equivalence Relation:
A relation $R$ on a set $A$ is called an equivalence relation if it is reflexive, symmetric and transitive.
Equivalence Class:
Let $R$ be an equivalence relation on a set $A$. The set of all elements that are related to an element $a$ of $A$ is called the equivalence class of $a$, denoted by $[a]_R$. When only on relation is considered, we use the notation $[a]$.
Let $R$ be an equivalence relation on a set $A$. The following statements are equivalent:
- $a\ R\ b$
- $[a]=[b]$
- $[a]\cap[b]\ne0$
Proof:
1→2: Prove $[a]\subseteq[b]$ and $[b]\subseteq[a]$
2→3: $[a]$ is not empty ($R$ reflexive)
3→1: $\exists c$ s.t. $c\in[a]$ and $c\in [b]$
Partition of a set:
Let $S$ be a set. A collection of nonempty subsets of $S$ $A_1,A_2,\cdots,A_k$ is called a partition of $S$ is
$A_i\cap A_j=\emptyset$, $i\ne j$ and $S=\bigcup\limits_{i=1}^{k}A_i$
Equivalence Classes and Partitions:
Let $R$ be an equivalence relation on a set $A$. Then union of all th equivalence classes of $R$ is $A$:
The equivalence classes form a partition of $A$.
Let $\{A_1,A_2,\cdots,A_i,\cdots\}$ be a partition of $S$. Then there is an equivalence relation $R$ on $S$, that has the sets $A_i$ as its equivalence classes.
Partial Ordering:
A relation $R$ on a set $S$ is called a partial ordering, if it is reflexive, antisymmetric and transitive. A set $S$ together with a partial ordering $R$ is called a poset, denoted by $(S,R)$. Members of $S$ are called elements of the poset.
Comparability:
The elements $a$ and $b$ of a poset $(S,≼)$ are comparable if either $a≼b$ or $b≼a$. Otherwise, $a$ and $b$ are called incomparable.
Total Ordering:
If $(S,≼)$ is a poset and every two elements of $S$ are comparable, $S$ is called a totally ordered or linearly ordered set, and $≼$ is called a total order or a linear order. A totally ordered set is also called a chain.
Lexicographic Ordering:
Given two posets $(A_1,≼_1)$ and $(A_2,≼_2)$, the lexicographic ordering on $A_1\times A_2$ is defined by specifying that $(a_1,a_2)$ is less than $(b_1,b_2)$, i.e., $(a_1,a_2)≼(b_1,b_2)$, either if $a_1≺_1b_1$ or if $a_1=b_1$ then $a_2≼_2b_2$.
Hasse Diagram:
……
Maximal and Minimal Elements:
$a$ is a maximal (resp. minimal) element in poset $(S, ≼)$ is there is no $b\in S$ such that $a ≺ b$ (resp. $b ≺ a$).
Greatest and Least Elements:
$a$ is the greatest (resp. least) element of the poset $(S, ≼)$ if $b ≼ a$ (resp. $a ≼ b$) for all $b\in S$.
Upper Bound and Lower Bound:
$u\in S$ is called an upper bound (resp. lower bound) of $A$ if $a ≼ u$ (resp. $u ≼ a$) for all $a\in A$.
$x\in S$ is called the least upper bound (resp. greatest lower bound) of $A$ if $x$ is an upper bound (resp. lower bound) that is less than any other upper bound (resp. greater than any other lower bound) of $A$.
Well-Ordered Set:
$(S, ≼)$ is a well-ordered set if it is a poset such that $≼$ is a total ordering and every non empty subset of $S$ has a least element.
The Principle of Well-Ordered Induction:
Suppose that $S$ is a well-ordered set. Then $P(x)$ is true for all $x\in S$, if
Inductive Step: For every $y\in S$, if $P(x)$ is true for all $x\in S$ with $x ≺ y$, then $P(y)$ is true.
The reason for no base step: For the least element $x_0$, the precedent “P(x) is true for all $x\in S$ with $x ≺ x_0$” is itself false, by vacuous proof, $P(x_0)$ is true.
Lattices:
A poset in which every pair of elements has both a least upper bound and a greatest lower bound is called a lattice.
Topological Sorting:
Given a partial ordering $R$, find a total ordering $≼$ such that $a≼b$ whenever $a\ R\ b$. $≼$ is said compatible with $R$.

Chapter 13 - Graph
Definition of a Graph:
A graph $G=(V,E)$ consists of a nonempty set $V$ of vertices and a set $R$ of edges. Each edge has either one or two vertices associated with it, called its endpoints. An edge is said to be incident to its endpoints.
Simple graph:
A graph in which at most one edge joins each pair of distinct vertices and no edge joins a vertex to itself.
multigraph:
Graphs that may have multiple edges connecting the same vertices.
pseudograph:
Graphs that may include loops, and possibly multiple edges connecting the same pair of vertices or a vertex to itself.
Undirected Graphs:
adjacent(neighbors), neighborhood, degree…
Handshaking Theorem: If $G=(V,E)$ is an undirected graph with $m$ edges, then $2m=\sum\limits_{v\in V}deg(v)$.
An undirected graph has an even number of vertices of odd degree.
Directed Graphs:
adjacent from, adjacent to, in-degree $deg^-(v)$, out-degree $deg^+(v)$
$|E|=\sum\limits_{v\in V}deg^-(v)=\sum\limits_{v\in V}deg^+(v)$
Complete Graphs:
A complete graph on $n$ vertices, denoted by $K_n$, is the simple graph that contains exactly one edge between each pair of distinct vertices.

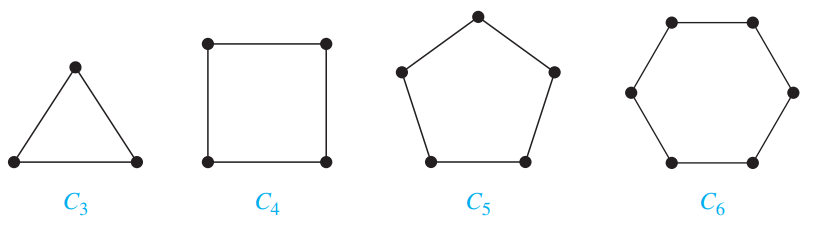
Cycles:
A cycle $C_n$ for $n \ge 3$ consists of $n$ vertices $v_1, v_2,\cdots, v_n$, and edges $\{v_1,v_2\},\{v_2,v_3\},\cdots,\{v_{n-1},v_n\},\{v_n,v_1\}$.
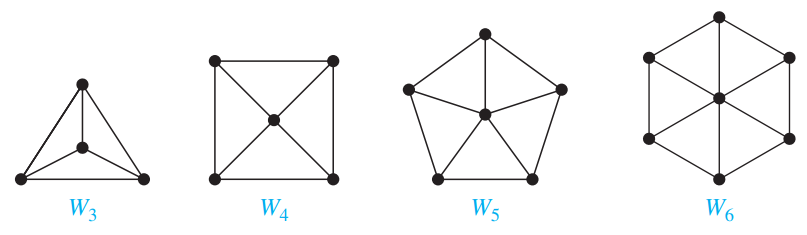
Wheels:
A wheel $W_n$ is obtained by adding an additional vertex to a cycle $C_n$.
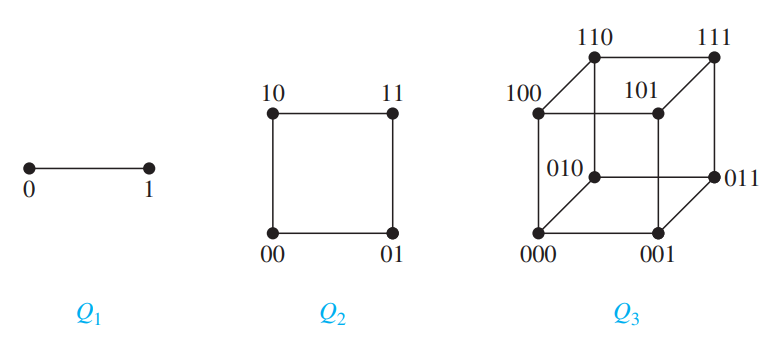
N-dimensional Hypercube:
An n-cube $Q_n$ is a graph with $2^n$ vertices representing all bit strings of length $n$, where there is an edge between two vertices that differ in exactly one bit position.
Bipartite Graphs:
A simple graph $G$ is bipartite if $V$ can be partitioned into two disjoint subsets $V_1$ and $V_2$ such that every edge connects a vertex in $V_1$ and a vertex in $V_2$.
Complete Bipartite Graphs:
A complete bipartite graph $K_{m,n}$ is a graph that has its vertex set partitioned into two subsets $V_1$ of size $m$ and $V_2$ of size $n$ such that there is an edge from every vertex in $V_1$ to every vertex in $V_2$.
Bipartite Graphs and Matchings:
A matching is a subset of $E$ such that no two edges are incident with the same vertex.
A maximum matching is a matching with the largest number of edges.
A matching $M$ in a bipartite graph $G=(V,E)$ wth bipartition $(V_1,V_2)$ is a complete matching from $V_1$ to $V_2$ if every vertex in $V_1$ is the endpoint of an edge in the matching, i.e., $|M|=|V_1|$.
Hall’s Marriage Theorem:
The bipartite graph $G=(V,E)$ with bipartition $(V_1,V_2)$ has a complete matching from $V_1$ to $V_2$ IFF $|N(A)|\ge |A|$ for all subsets $A$ of $V_1$.
“only if”: For every vertex $v\in A$, there is an edge in $M$ connecting $v$ to a vertex in $V_2$. Thus, for all subsets $A$ of $V_1$, there are at least as many vertices in $V_2$ that are neigbors of vertices in $A$ as there are vertices in $A$, $|N(A)|\ge |A|$.
“if”: Use strong induction.
Base step: $|V_1|=1$
Inductive hypothesis: Let $k$ be a positive integer. If $G=(V,E)$ is a bipartite graph ith bipartition $(V_1,V_2)$, and $|V_1|=j\le k$, then there is a complete matching $M$ from $V_1$ to $V_2$ whenever the condition that $|N(A)|\ge |A|$ for all $A\subseteq V_1$ is met.
Inductive step: suppose that $H=(W,F)$ is a bipartite graph with bipartition $(W_1,W_2)$ and $|W_1|=k+1$
Case (Ⅰ): For all integers $j$ with $1\le j\le k$, the vertices in every set of $j$ elements from $W_1$ are adjacent to at least $j+1$ elements of $W_2$.
Find a complete matching from $W_1-\{v\}$ to $W_2-\{w\}$, then match $v$ to $w$.
Case (Ⅱ): For some integer $j$ with $1\le j\le k$, there is a subset $W_1’$ of $j$ vertices such that there are exactly $j$ neighbors of these vertices in $W_2$.
Let $W_2’$ be the set of these neighbors. Then by i.h., there is a complete matching from $W_1’$ to $W_2’$. Now consider the graph $K=(W_1-W_1’,W_2-W_2’)$. We will show that the condition $|N(A)|\ge |A|$ is met for all subsets $A$ of $W_1-W_1’$.
If not, there is a subset $B$ of $t$ vertices with $1\le t\le k+1-j$ such that $|N(B)|<|B|$, contradiction.
Then there is a complete matching for $K$, and thus a complete matching for $G$.
Subgraphs:
A subgraph of a graph $G=(V,E)$ is a graph $(W,F)$, where $W\subseteq V$ and $F\subseteq E$. A subgraph $H$ of $G$ is a proper subgraph of $G$ if $H\ne G$.
Union of Simple Graphs:
Simple graph: $G_1\cup G_2=(V_1\cup V_2, E_1\cup E_2)$
Representation of Graphs:
adjacency lists, adjacency matrices, and incidence matrices.
Isomorphism of Graphs:
The simple graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ are isomorphic if there is a bijection from $V_1$ to $V_2$ with the property that $a$ and $b$ are adjacent in $G_1$ IFF $f(a)$ and $f(b)$ are adjacent in $G_2$, for all $a$ and $b$ in $V_1$. Such a function is called an isomorphism.
Useful graph invariants: the number of vertices, number of edges, degree sequence, etc.
Path:
Let $n$ be a nonnegative integer and $G$ an undirected graph. A path of length $n$ from $u$ to $v$ in $G$ is a sequence of $n$ edges $e_1,e_2,\cdots,e_n$ of $G$ for which there exists a sequence $x_0=u,x_1,\cdots,x_{n-1},x_n=v$ of vertices such that $e_i$ has the endpoints $x_{i-1}$ and $x_i$ for $i=1,\cdots,n$.
A path is simple if it does not contain the same edge more than once.
Circuit:
The path is a circuit if it begins and ends at the same vertex, i.e., if $u=v$ and has the length greater than $0$.
Simple Path Existence Lemma:
If there is a path between two distinct vertices $x$ and $y$ in graph $G$, then there is a simple path between $x$ and $y$ in $G$. (Just delete cycles/loops.)
Connected Components:
A connected component of a graph $G$ is a connected subgraph of $G$ that is not a proper subgraph of another connected subgraph of $G$.
Connectedness in Directed Graphs:
A directed graph is strongly connected if there is a path from $a$ to $b$ and a path from $b$ to $a$ whenever $a$ and $b$ are vertices in the graph.
A directed graph is weakly connected if there is a path between every two vertices in the underlying undirected graph.
Cut Vertices and Cut Edges:
……
A set of edges $E’$ is called an edge cut of $G$ if the subgraph $G-E’$ is disconnected. The edge connectivity $\lambda(G)$ is the minimum number of edges in an edge cut of $G$.
Paths and Isomorphism:
The existence of a simple circuit of length $k$ is isomorphic invariant. In addition, paths can be used to construct mappings that may be isomorphisms.
Counting Paths between Vertices:
Let $G$ be a graph with adjacency matrix $A$ with respect to the ordering $v_1, v_2,\cdots, v_n$ of vertices. The number of different paths of length r from $v_i$ to $v_j$ , where $r > 0$ is positive, equals the $(i, j)$-th entry of $A^r$.
Proof by induction:
$A^{r+1}=A^rA$, the $(i,j)$-th entry of $A^{r+1}$ equals $b_{i1}a_{1j}+b_{i2}a_{2j}+\cdots+b_{in}a_{nj}$, where $b_{ik}$ is the $(i,k)$-th entry of $A^r$.
Euler Paths and Circuits:
An Euler circuit in a graph $G$ is a simple circuit containing every edge of $G$.
A connected multigraph with at least two vertices has an Euler circuit IFF each of its vertices has even degree.
An Euler path in $G$ is a simple path containing every edge of $G$.
A connected multigraph has an Euler path but not an Euler circuit IFF it has exactly two vertices of odd degree.
Hamilton Paths and Circuits:
A simple path in a graph $G$ that passes through every vertex exactly once is called a Hamilton path.
A simple circuit in a graph $G$ that passes through every vertex exactly once is called a Hamilton circuit.
Sufficient Conditions for Hamilton Circuits:
Dirac’s Theorem: If $G$ is a simple graph with $n\ge 3$ vertices such that the degree of every vertex in $G$ is $\ge n/2$, then $G$ has a Hamilton circuit.
Ore’s Theorem: If $G$ is a simple graph with $n\ge 3$ vertices such that $deg(u)+deg(v)\ge n$ for every pair of nonadjacent vertices, then $G$ has a Hamilton circuit.
Shortest Path Problems:
Dijkstra-$O(v^2)$, Fredman & Tarjan-$O(e+v\log v)$, Bellman-Ford-$O(ev)$…
Planar Graphs:
A graph is called planar if it can be drawn in the plane without any edge crossing. Such a drawing is called a planar representation of the graph.
Euler’s Formula:
Let $G$ be a connected planar simple graph with $e$ edges and $v$ vertices. Let $r$ be the number of regions ina planar representation of $G$. Then $r=e-v+2$.
Proof by induction.
The Degree of Regions:
The degree of a region is defined to be the number of edges on the boundary of this region. When an edge occurs twice on the boundary, it contributes two to the degree.
Corollaries of Planar Graphs:
Corollary 1: If $G$ is a connected planar simple graph with $e$ edges and $v$ vertices, where $v\ge3$, then $e\le 3v-6$.
The degree of every region is at least 3.
The sum of the degrees of the regions is exactly twice the number of edges in the graph.
Corollary 2:If $G$ is a connected planar simple graph, then $G$ has a vertex of degree not exceeding 5.
- Proof by contradiction using Corollary 1 and Handshaking Theorem.
Corollary 3:In a connected planar simple graph has $e$ edges and $v$ vertices with $v\ge3$ and no circuits of length 3, then $e\le2v-4$.
- The degree of every region is at least 4. (no circuit of length 3)
Kuratowski’s Theorem:
If a graph is planar, so will be any graph obtained by removing an edge $\{u, v\}$ and adding a new vertex $w$ together with edges $\{u,w\}$ and $\{w, v\}$. Such an operation is called an elementary subdivision.
The graphs $G_1 = (V_1, E_1 )$ and $G_2 = (V_2, E_2 )$ are called homomorphic if they can be obtained from the same graph by a sequence of elementary subdivisions.
A graph is nonplanar IFF it contains a subgraph homomorphic to $K_{3,3}$ or $K_5$.
Graph Coloring:
A coloring of a simple graph is the assignment of a color to each vertex of the graph so that no two adjacent vertices are assigned the same color.
The chromatic number of a graph is the least number of colors needed for a coloring of this graph, denoted by $\chi(G)$.
Four-color theorem:
The chromatic number of a planar graph is no greater than 4.
Six Color Theorem:
The chromatic number of a planar graph is no greater than 6.
Proof by induction. (w.l.o.g., assume that the graph is connected)
Basic step: For a single vertex, pick an arbitrary color.
Inductive hypothesis: Assume that every planar graph with $k\ge1$ or fewer vertices can be 6-colored.
Inductive step: Consider a planar graph with $k+1$ vertices. Using Corollary 2 (the graph has a vertex of degree 5 or fewer). Remove this vertex, by i.h., we can color the remaining graph with 6 colors. Put the vertex back in. Since there are at most 5 colors adjacent, so we have at least one color left.
Five Color Theorem:
The chromatic number of a planar graph is no greater than 5.
Proof by induction. (w.l.o.g., assume that the graph is connected)
Basic step: For a single vertex, pick an arbitrary color.
Inductive hypothesis: Assume that every planar graph with $k\ge1$ or fewer vertices can be 5-colored.
Inductive step: Consider a planar graph with k + 1 vertices. Using Corollary 2 (the graph has a vertex of degree 5 or fewer). Remove this vertex, by i.h., we can color the remaining graph with 5 colors. Put the vertex back in.
Case (Ⅰ): If the vertex has degree less than 5, or if it has degree 5 and only $\le 4$ colors are used for vertices connected to it, we can pick an available color for it.
Case (Ⅱ): We make a subgraph out of all the vertices colored 1 or 3. If the adjacent vertex colored 1 and the adjacent vertex colored 3 are not connected by a path in the subgraph.
On the other hand, if the vertices colored 1 and 3 are connected via a path in the subgraph, we do the the same for the vertices colored 2 and 4. Note that this will be a disconnected pair of subgraphs, separated by a path connecting the vertices colored 1 and 3.
Chapter 14 - Tree
Tree:
A tree is a connected undirected graph with no simple circuits.
An undirected graph is a tree IFF there is a unique simple path between any two of its vertices.
A rooted tree is a tree in which one vertex has been designated as the root and every edge is directed away from the root.
parent, child, sibling, ancestor, descendant, leaf, internal vertex, subtree…
m-Ary Trees:
A rooted tree is called an m-ary tree if every internal vertex has no more than $m$ children.
The tree is called a full m-ary tree if every internal vertex has exactly $m$ children.
In particular, an m-ary tree with $m = 2$ is called a binary tree.
A binary tree is an ordered rooted tree where the children of each internal vertex are ordered.
In a binary tree, the first child is called the left child, and the second child is called the right child.
left subtree, right subtree
Counting Vertices in a Full m-Ary Trees:
A full m-ary tree with $i$ internal vertices has $n = mi + 1$ vertices. Leaves number $ℓ=n-i$.
Level and Height:
The level of a vertex $v$ in a rooted tree is the length of the unique path from the root to this vertex.
The height of a rooted tree is the maximum of the levels of the vertices.
A rooted m-ary tree of height $h$ is balanced if all leaves are at levels $h$ or $h − 1$. (differ no greater than 1)
The Number of Leaves:
There are at most $m^h$ leaves in an m-ary tree of height $h$.
If an m-ary tree of height $h$ has ℓ leaves, then $h \ge ⌈\log_m ℓ⌉$. If the m-ary tree is full and balanced, then h = $⌈\log_mℓ⌉$.
Tree Traversal:
preorder traversal, inorder traversal, postorder traversal.
expression trees, prefix notation, infix notation, postfix notation.
Catalan Numbers:
$C_0=C_1=1$
$C_n=\sum\limits_{i=0}^{n-1}C_iC_{n-i-1}=\frac{1}{n+1}\left(\begin{array}{c}2n \\n\end{array}\right)=\left(\begin{array}{c}2n \\n\end{array}\right)-\left(\begin{array}{c}2n \\n-1\end{array}\right)$
The number of 01 sequences using $n$ ones and $n$ zeros such that the number of ones is no less than the number of zeros in any prefix subsequence.
The number of full binary trees with $2n+1$ vertices.
The number of binary trees with $n$ vertices.
Spanning Trees:
Let $G$ be a simple graph. A spanning tree of $G$ is a subgraph of $G$ that is a tree containing every vertex of $G$.
A simple graph is connected IFF it has a spanning tree.
DFS, BFS:
……
Minimum Spanning Trees:
Prim’s Algorithm($O(e\log v)$), Kruskal’s Algorithm($O(e\log e)$).
Chapter 15 - P, NP and NPC Problems
Class NP vs. Class P:
P: decision problems solvable in polynomial time
NP: decision problems with certificates verifiable in polynomial time (polynomial time verification)
Satisfiability Problem(NP):
To determine whether a Boolean formula is satisfiable or not.
2SAT Problem(P):
To determine whether a 2-CNF formula is satisfiable or not.
Using path searching (polynomial-time decidable), construct edges using “→”.
A 2-CNF formula is unsatisfiable IFF there exists a variable $x$ such that:
- there is a path from $x$ to $\neg x$ in the graph $G$
- there is a path from $\neg x$ to $x$ in the graph $G$
Polynomial-Time Reduction & The Class NP-Complete:
see Chapter 6.
Cook’s Theorem:
SAT $\in$ NPC.
3SAT $\le_P$ DCLIQUE $\le_P$ DVC
Clique:
A clique is a complete subgraph of $G$.
The Problem CLIQUE
Find a clique of maximum size in a graph $G$.
The Problem DCLIQUE
Given an undirected graph G and an integer $k$, determine whether $G$ has a clique of size $k$.
DCLIQUE $\in$ NP: certificate $O(|V^2|)$
3SAT $\le_{P}$ DCLIQUE:
For the $k$ clauses input to 3SAT, draw literals as vertices, and all edges between vertices such that:
- across clauses only
- not between $x$ and $\neg x$
The reduction takes polynomial time: A satisfiable assignment $⇌$ a clique of size $k$
Vertex Cover:
A vertex cover of $G$ is a set of vertices such that every edge in $G$ is incident at at least one of these vertices.
The Vertex Cover Problem (VC)
Given a graph $G$, find a vertex cover of $G$ of minimum size.
The Problem DVC
Given a graph $G$ and an integer $k$, determine whether $G$ has a vertex cover of with $k$ vertices.
DVC $\in$ NP: certificate $O(ke)=O((n+e)^2)$
DCLIQUE $\le_{P}$ DVC:
Start with the graph $G=(V,E)$ input of the DCLIQUE problem.
Construct the complement graph $\bar G=(V,\bar E)$ by only considering the missing edges from $E$.
The reduction takes polynomial time: A clique of size $k$ in $G$ $⇌$ a vertex cover of size $|V|-k$ in $\bar G$
Approximate Vertex Cover:
Approx-Vertex-Cover is a 2-approximation algorithm, i.e., $\frac{|C|}{|C^\star|}\le 2$.
Proof:
The set of edges picked by this algorithm is a maximal-maching $M$: no two edges touch each other.
The potimal vertex cover $C^\star$ must cover every edge in $M$, so $|C^\star|\ge |M|$. The algorithm returns a vertex set of size $2|M|$. Therefore, we have
.
