$\huge\text{Outline}$
- 人工智能概述
- 搜索
- 启发与元启发
- 对抗搜索
- 约束满足问题
- 逻辑
- 机器学习概述
- 线性回归与对数回归
- 支持向量机
- 感知机与神经网络
- 决策树与朴素贝叶斯
- 集成学习与聚类
- 强化学习
- 自然语言处理
Chapter 1 - 人工智能概述
第一课略,大致是概念的介绍和AI发展的介绍。
智能体
智能体的特征
通过探测器感知环境
perceiving its environment through sensors
根据环境利用执行器执行操作
acting upon that environment through actuators
智能体运行周期:感知(perceive),思考(perceive),行动(act)
智能体是Architecture和Program的互补兼容。
Rationality的评价标准:PEAS
- Performance
- Environment
- Actuators
- Sensors
智能体的类型
Simple reflex agents
只根据当前状态决策行动,需要完全可观测环境,且正确行动只与当前观测有关。
Model-based reflex agents
智能机内部状态由历史观测决定,可以处理部分可观测环境
建立环境模型:环境如何独立演变 + 行动如何影响环境
Goal-based agents
拥有目标信息,考虑每种行动对接近目标的贡献
Utility-based agents
Utility function评估智能体性能,选择最大化期望utility的行动
Learning agents
Learning element:根据输入进行提升
Performance element:选择执行的行动
Critic:由固定的性能评估标准决定智能体的表现
Problem Generator:允许智能体进行探索
智能体的状态
原子表示Atomic Representation
每个环境状态都是不具有内部结构的黑盒
Search, games, Markov decision processes, hidden Markov models, etc
因子表示Factored Representation
每个状态都有一些属性,可以用一组变量来表示
Constraint satisfaction, and Bayesian networks.
结构表示Structured Representation
状态之间的关系可以显式表达
First order logic, knowledge-based learning, natural language understanding.
环境
环境的类型
完全可观测Fully observable/部分可观测Partially observable
确定Deterministic/随机Stochastic
下一步的环境是否只由Agent的行动和当前环境决定。
Episodic/Sequential
前者说明每一步行动不影响下一步,后者说明会影响。
静态Static/动态Dynamic
环境在智能体运行时是否变化(半动态:环境不变,但评分变动)
离散Discrete/连续Continuous
单智能体Single-agent/多智能体Multi-agent
已知Known/未知Unknown
设计者是否拥有对环境的知识
Chapter 2 - 搜索
搜索概述
通过搜索解决问题
定义问题
(a)目标形式化
(b)问题形式化
两步解决问题
(a)离线搜索不同行动
(b)执行搜索结果
问题形式化
- 初始状态
- 状态:所有由初始状态,通过任意行动序列可达的状态集合(状态空间)
- 行动:对于一个状态,智能体可以执行的所有行动(行动空间)
- 转化模型:描述每个行动对当前状态造成的影响
- 目标检测:决定给定状态是否已经达到目标
- 路径开销:根据性能标准为动作序列赋上数值开销的函数
状态空间 vs. 搜索空间
状态空间是实际状态的集合
搜索空间是抽象成搜索树/图的可行解集合
搜索树描述了行动序列
根节点:初始状态
分支:行动
结点:行动的结果
每个结点有:父节点,子节点,深度,路径开销,在状态空间对应的状态
扩张Expand:对于给定结点,创建所有子结点的函数
搜索空间的三个区域
- Explored (a.k.a. Closed List, Visited Set)
- Frontier (a.k.a. Ready list, Open List, the Fringe)
- Unexplored
搜索就是从3到2再到1的过程,搜索策略决定了顺序。
搜索策略
搜索策略由选定结点进行扩张的顺序来定义,评价标准:
- 完备性Completeness
- 时间复杂度Time complexity
- 空间复杂度Space complexity
- 最优性Optimality
时间复杂度和空间复杂度的评估:
- $b$ - 搜索树最大的分支数量
- $d$ - 解的深度
- $m$ - 状态空间的最大深度
无信息搜索
不使用domain knowledge的搜索。
Breadth-first search / 广度优先 / BFS
优先探索最浅的结点
Depth-first search / 深度优先 / DFS
优先探索最深的结点
Depth-limited search / 深度限制 / DLS
带深度限制的DFS
Iterative-deepening search / 迭代加深 / IDS
不断放宽深度限制(提高深度上限)的DLS
Uniform-cost search (UCS) / 统一代价 / UCS
优先探索开销最小的结点(参考Dijkstra)
| 完备性 | 时间 | 空间 | 最优性 | 实现 | |
|---|---|---|---|---|---|
| BFS | 有限分支则完备 | $O(b^d)$ | $O(b^d)$ | 每步开销都为1则最优 | Queue |
| DFS | 有限状态空间则完备 | $O(b^m)$ | $O(bm)$ | 否 | Stack |
| UCS | 有限开销则完备 | $O(b^{C^*/\epsilon})$ | $O(b^{C^*/\epsilon})$ | 是 | Heap |
* 其中$C^*$是最优解的开销,每一步行动至少开销$\epsilon$
有信息搜索
使用领域知识来获取关于当前状态与目标距离的信息。
贪心BFS
把到目标的估计费用$h(n)$当作唯一标准贪心搜索
A*搜索
$f(n)=$到当前结点的费用$g(n)$+当前结点到目标的估计费用$h(n)$
$f(n)$是经过结点$n$的最优路径费用的估值
完备性:是
时间复杂度:指数级
空间复杂度:每个结点都在内存里,最大的问题
最优性:是
可接受的启发函数(Admissible heuristics)
如果启发式函数从不高估到达目标的费用,那么就是可接受的(admissible),并且使用该启发式函数的A*得到的解是最优的。
证明:
Suppose $G_o$ is the optimal goal.
Suppose $G_s$ is some suboptimal goal.
Suppose $n$ is on the shortest path to $G_o$.
$f(G_s) = g(G_s)$ since $h(G_s) = 0$
$f(G_o ) = g(G_o )$ since $h(G_o ) = 0$
$g(G_s)>g(G_o )$ since $G_s$ is suboptimal
Then $f(G_s) > f(G_o ) . . . (1)$
$h(n)\le h^*(n)$ since h is admissible
$g(n)+h(n)\le g(n)+h^* (n) = g(G_o ) = f(G_o )$
Then $f(n) \le f(G_o ) . . . (2)$
From (1) and (2) $f(G_s)>f(n)$, so A* will never select $G_s$ during the search and hence A* is optimal.
IDA*搜索
把迭代加深方法加到A*搜索上。
局部搜索
不关心到目标的路径,优化问题可以使用局部搜索。
只维护当前状态,并通过移动到相邻状态,试图优化。
- 不需要维护搜索树
- 内存占用小
- 在连续或较大的状态空间中找到较好解
爬山算法
贪心局部搜索,只选择最优的邻居进行探索,到达峰值时停止(可能是局部峰值)
每个结点代表一个状态和一个值
变种:
- Sideways moves 允许转移到与当前状态同等优的解
- Random-restart 多试几次取最优
- Stochastic 随机选择不同的上坡算子
改进:
- Hill climbing:取决于地形,多重开几次还是不错的
- Local beam search:同时维护前k优的解,探索其邻居
- Stochastic beam search:随机选择k个解(不一定是前k优),探索其邻居
遗传算法
Stochastic beam search的变种。
自然选择,种群,个体,基因,健壮函数,交叉互换,后代,变异
模拟退火
温度指数级下降,以一定概率接受较劣解,温度越高跳出当前解的可能性越高。
接受概率:$P = e^{-\Delta E/T}$
Chapter 3 - 启发与元启发
启发式函数进阶
启发式函数与效率
如果一个启发式函数始终不小于另一个启发式函数,称其为dominate,前者拥有更好的效率。好的启发式函数可以降低$b^\star$,分支数量化了启发式搜索的效率。
对于一堆admissible的启发式函数$\{h_i\}$,能够dominate所有函数的是$\max\{h_i\}$。
好的启发式函数上哪找?
- 从放宽条件的问题入手,例如8-puzzle允许块之间重叠,得到的步数总是要比原问题少的。
- 从子问题入手,例如8-puzzle只把一部分块归位而不管其他的。该问题中,函数$h_{\text{sub}}$(只考虑四块的启发式函数极大值并集)是dominate函数$h_{1step}$的。
- 根据经验生成,可以选定当前状态的几个特征作为变量,用神经网络/决策树来学这些变量对应的权重,用线性函数表示启发式函数
元启发式函数进阶
与问题相互独立的启发式方法,可以组合使用。
One general law, leading to the advancement of all organic beings, namely, multiply, vary, let the strongest live and weakest die.
Charles Darwin, The Origin of Species
演化计算:繁殖,变异,选择
Chapter 4 - 对抗搜索
Minimax搜索
其中某一方,按照双方都足够聪明的情况进行DFS(DLS),从搜索树所有分支中选择对各自最优的。
在可以搜索到终局的情况下,对于一个状态$s$,minimax函数:
然而博弈是有时限的,指数级时间复杂度不可能搜完,所以:
- 将终局评估改成非终局评估
- 使用迭代加深搜索IDS
- 剪枝
$\alpha-\beta$ 剪枝
$\alpha$:$\text{MAX}$结点目前已经探索的结点中最大的一个。当前结点不会探索比$\alpha$估值还低的结点。
$\beta$:$\text{MIN}$结点目前已经探索的节点中最小的一个。当前结点不会探索比$\beta$估值还高的结点。
什么时候要剪呢?
$\text{MAX}$视角:$\text{MIN}$在再下一步的结点中,发现了比$\alpha$还低的值,那$\text{Min}$肯定会选这个分支,导致$\text{MAX}$的估值小于$\alpha$,为了避免这种局面,当下一层的$\text{MIN}$发现了一个比$\alpha$还小的值时,说明对手足够聪明的情况下,$\text{MAX}$在这一分支会被对手限制到不如$\alpha$的局面,剪掉。
$\text{MIN}$视角:$\text{MAX}$在再下一步的结点中,发现了比$\beta$还大的值,那$\text{MAX}$肯定会选这个分支,导致$\text{MIN}$的估值大于$\beta$,为了避免这种局面,当下一层的$\text{MAX}$发现了一个比$\beta$还大的值时,说明对手足够聪明的情况下,会选择这个新的分支规避$\beta$的限制,故剪掉。
“自裁式”实现
上面的说法更像是当前结点主动剪子结点。但还有一种“自裁式”的剪法,就是某个结点发现自己太好了,肯定会被足够聪明的上一层剪掉,就自裁了。
搜索的时候,父结点把自己的$\alpha-\beta$给子结点,探索完一个子结点后,做如下操作:
当前节点是$\text{MAX}$,如果$\text{MIN}$子结点给出的估值比当前最高的还高,那就检查有没有超过当前节点的$\beta$,如果超过了当前节点的$\beta$,说明当前这一支太好了,会被更高层的$\text{MIN}$掐掉,所以这个$\text{MAX}$结点就被整个剪掉了;如果没超过$\beta$而且还比当前最高还高,那就更新当前的最高值和$\alpha$。
当前节点是$\text{MIN}$时同理,如果这个$\text{MIN}$结点能把最优解掐到不足$\alpha$,那$\text{MIN}$结点的$\text{MAX}$父节点肯定不乐意啊,所以一整个$\text{MIN}$结点就被剪掉了。

换序剪枝
$\alpha-\beta$ 剪枝的效果受访问顺序影响,有可能导致剪枝的结点最后才被访问,这就剪了个寂寞。
最差的顺序相当于没有剪枝,复杂度是$O(b^m)$。
最好的顺序则是把最“聪明”的结点都放在最先访问,实际复杂度是$O(b^{m/2})$,直接开了个根号。
如何找到一个好的顺序呢?除了动用领域知识,还可以保存历史表,以前发现最好的几步可能在之后还是最好的几步,或是保存状态以供重复时使用。
实际情况
上面的$\alpha-\beta$剪枝伪代码还是要一直搜到叶子结点,依然是不现实的,所以将$\text{Util(s)}$函数更换为可以评价中局的启发式函数$\text{eval(s)}$。
期望Minimax搜索
对于带有随机性的博弈,期望Minimax搜索在$\text{MIN}$和$\text{MAX}$之外又加入了$\text{Chance}$层,会返回当前所有可能发生的情况合起来的期望。
其中$r$代表了所有的随机事件。
Chapter 5 - 约束满足问题
CSP概述
也是搜索问题,但是我们更关心目标本身。
CSP的状态是因子表示的,也就是由一组变量表示。
一个目标测试(goal test)是对于这组变量(的子集)的一组限制。
CSP问题的三个要素
- 变量集合$X$
- 变量定义域的集合$D$
- 约束的集合$C$
CSP的解:在定义域$D$中,对变量$X$找到一个合适的赋值方案$s$,满足所有的约束$C$。这样的解称为一致的赋值(consistent assignment)。
变量类型:离散/连续
限制类型:一元(unary),二元(binary),全局(global),偏好/软限制(preferences/soft constraints)
解决CSP
暴力太慢,配合推理(inference)和搜索(search)来加速。
Inference主要是约束传播(constraint propagation),是指一个变量的合法取值变少时,其他变量的合法取值也会变少。
Search的DFS和BFS都是老朋友了,新来了个BTS。
回溯搜索(Backtracking search, BTS)也是一种DFS,满足以下条件:
- 一次赋一个变量的值:赋值顺序是可交换的
- 赋值的时候就注意和之前的赋值不能冲突
感觉和DFS没区别啊= =
改进BTS的三种方法
最小剩余值(Minimum Remaining Value)
Q:先给哪个变量赋值?
先挑硬柿子捏
每次挑剩余选择最少的结点赋值。
最小限制值(Least Constraining Value)
Q:给这个变量赋哪个值?
少给后人添麻烦
每次挑对别人限制最少的结点赋值。
前向检查(Forward Checking)
Q:世界末日是可预见的吗?
关心每个人的未来
每次赋值后检查所有未赋值变量定义域是否为空。
在前向检查的时候用到了约束传播的思想,用已赋值的变量去限制未赋值的变量,看还有没有合法赋值,不过这里并不做未赋值变量之间的检查。
一致性
点一致性(一元限制)
如果一个点的定义域内所有的值都满足所有的一元限制,那它拥有点一致性
弧一致性(二元限制)
两个变量$X\rightarrow Y$具有弧一致性,当且仅当对$X$的每个值都有对应的$Y$的值满足二元条件。
弧一致性检验
AC-3算法,复杂度$O(n^2d^3)$。
$\text{REVISE()}$函数根据给定的两个变量,将第一个变量定义域中找不到第二个变量定义域对应值的值删掉,只有删了至少一个值的时候才会返回真,说明需要对前者的邻居再进行$\text{REVISE}$,复杂度$O(d^2)$,$d$是定义域大小。
$\text{AC-3()}$函数维护一个初始包含所有弧的队列,每次取出一个做$\text{REVISE}$,如果前变量的定义域缩小了,那就用它接着更新它的其他邻居,直到所有弧都出队(被满足),或是有一个点的定义域被删干净了(不满足)。
1 | function AC-3(csp) |
路径一致性(多元限制)
弧一致性的多元推广。
Chapter 6 - 逻辑
经过了数理逻辑导论和离散数学的洗礼我觉得这部分还是得复习一下,至少要知道Resolution和Forward/Backward Chaining怎么证。
铺垫
原子命题,复合命题,逻辑算符,重言式与矛盾式
Inference: Modus Ponens
Common Rules: Addition, Simplification, Disjunctive-syllogism, Hypothetical-syllogism
Entailment, Semantics: KB ⊨ α
Inference, Syntax: KB ⊢ α
Sound & Complete, Validity & Satisfiability
Resolution
使用Resolution rule:一堆$\vee$连接的文字中的某个文字的否命题与其同时成立,则可以将该文字剔除。
一般转成合取范式(CNF)再用Resolution rule。
Forward / Backward chaining
在霍恩子句上用Modus Ponens。
前向链接:把已知逻辑式塞到所有规则的前提里,把结论塞回知识库,直到解决问题。对命题逻辑是完备的。
- 数据驱动,自动化,无意识推理
- 可能做很多无用功
后向链接:为了得到问题的结论,需要得到问题的前提,递归证明前提。可以做记忆化。时间上是线性的,对霍恩子句是完备的。
- 目标驱动,适用于解决问题
- 复杂度会远远小于$O(|\text{Knowledge Base}|)$
一阶逻辑? Nobody cares(
Chapter 7 - 机器学习概述
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
Tom Mitchell. Machine Learning 1997.
无监督学习
无监督学习:训练样本没有标签
应用:聚类,切割
算法:K-means, Gaussian mixtures, hierarchical clustering, spectral clustering, etc.
监督学习
监督学习:训练样本带有对应的标签
应用:分类(样本→离散),回归(样本→连续)
分类算法:Support Vector Machines, neural networks, decision trees, K-nearest neighbors, naïve Bayes, etc.
K近邻
两个相似的样本应该拥有相同的标签。
每个样本视为$d$维空间的点,距离用欧氏距离表示。
训练算法:直接把样本和标签丢到训练集就行
分类算法:给定一个测试样本,看看距离它最近的$k$个样本标签是什么,哪个标签样本数多,测试样本就被分到哪个标签。
优点:
- 简单
- 实际效果好
- 不需要建立模型,或者做假设,又或者调参
- 有新样本很快就扩展了
缺点:
- 需要很大的空间来存整个训练集
- 慢,给定$n$样本$d$特征,需要$O(nd)$才能跑出来
- 维数灾难:样本分布位于中心附近的概率,随着维度的增加,越来越低;而样本处在边缘的概率,则越来越高。
Train, Validation and Test
样本内误差:
损失函数$\text{loss()}$可以是分类误差(不一样时1),也可以是均方误差(差值平方和)
目标是最小化训练误差,同时希望样本外误差(测试误差)最小。
过拟合和欠拟合
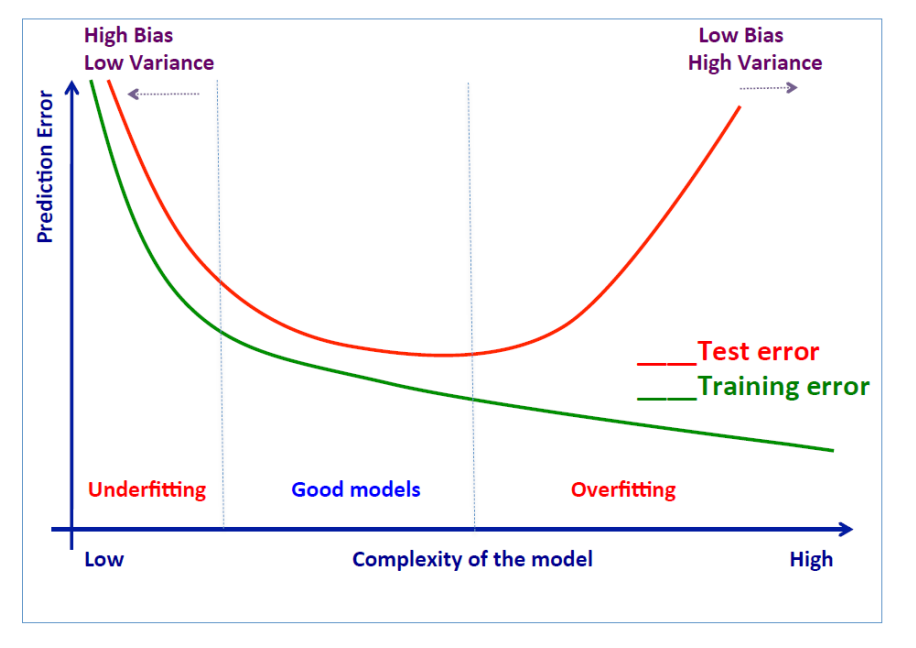
这幅图蛮重要的,嗯。
如何避免过拟合?
- 减少特征数量:特征选择
- 模型选择
- 正则化(regularization):削弱部分特征的重要程度
- 做交叉验证(cross-validation),检验测试误差
正则化
最小化:$\sum_{i=1}^{n} \operatorname{loss}\left(y_{i}, f\left(x_{i}\right)\right)+C \times R(f)$
目标是避免高阶多项式的出现
Train, Validation and Test
把数据集分成三部分,训练集给样本给标签,验证集给样本看结果用来调参,测试集用来评估最终性能。
K-fold交叉验证
把数据集分成等大的$k$个子集,每次把其中一个挑出来用来当测试集算误差,最后把所有的误差再加起来。
混淆矩阵(Confusion matrix)
| Actual | Label | |
|---|---|---|
| Predicted | True Positive | False Positive |
| Label | False Negative | True Negative |
Accuracy: $\text{(TP+TN)/Total}$
Precision: $\text{TP/(TP+FP)}$
Sensitivity: $\text{TP/(TP+FN)}$
Specificity: $\text{TN/(TN+FP)}$
Chapter 8 - 线性回归与对数回归
线性回归
$f(x) = \beta_0 + \sum\limits_{j=1}^d \beta_jx_j$,其中$\beta_j\in \mathbb R,\ j\in \{1,\cdots,d\}$
学习线性模型其实就是学习$\beta$。
最小化损失函数$R$:
如果用矩阵形式表示:
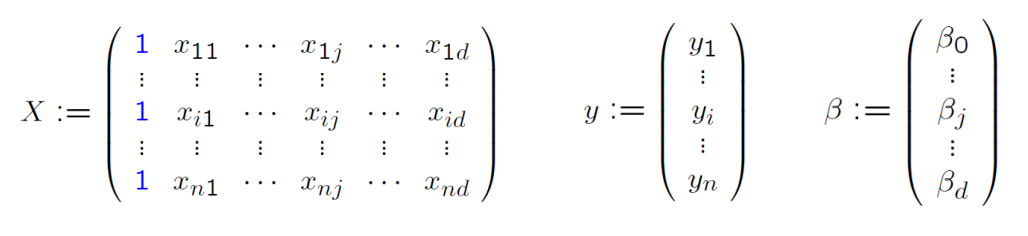
正规方程
我们有$R(\beta) = \frac{1}{2n}||(y-X\beta)||^2 = \frac{1}{2n}(y-X\beta)^T(y-X\beta)$,求偏导有
二阶偏导为正,说明正定,令一阶偏导为0求得$\beta_\min = (X^TX)^{-1}X^Ty$
优点:不用定义收敛率,也不用迭代
缺点:需要保证$X^TX$可逆;当维数$d$很高的时候求逆是$O(d^3)$的,很慢。
梯度下降
同时让$\beta$的每个分量沿着梯度下降:
$\beta_i = \beta_i-\alpha \frac{\partial R}{\partial \beta_i}$,其中$\alpha$是学习率。
优点:高维依然很管用
缺点:需要迭代,有时候迭代很多代才收敛;需要调参$\alpha$
实际考虑
- 一般会把数据做个归一化,把数据变小点
- 学习率不能太大,也不能太小
- 损失函数应该随着迭代递减
- 如果优化程度在$\epsilon$之内说明收敛了
- 什么时候$X^TX$不可逆?
- 样本过少,特征过多
- 特征之间线性相关
对数回归
做分类,线性回归也不是不行,只是表现一般,而且预测值有时候又不在$[0, 1]$之间。
对数回归不是一个回归方法,而是一个分类方法,虽然怪怪的但是课件原话。
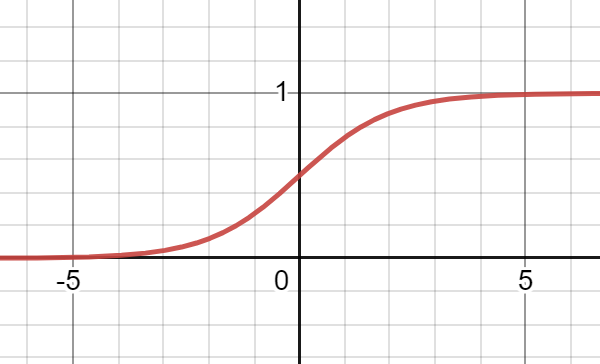
对数回归用的$f$就不太一样了,相当于是把输出映射到了$[0,1]$
分类的时候,离哪边近就分到哪边。
旧损失函数$\text{Loss}=\frac 1 2(f(x)-y)^2$这个时候就不是简单的二次函数了,可能有很多局部最优,所以对旧损失函数的梯度下降寄了。为了全局最优,对损失使用凸函数罢!
所以有损失函数:
好了,我们又可以梯度下降了。
Chapter 9 - 支持向量机
线性模型
线性模型的分类靠超平面:$f(x)=\left \langle w,x\right \rangle+b=0$
支持向量机要求所有点都在正负超平面之外(含超平面),正负超平面:$\left \langle w,x\right \rangle+b=±c$
不过我们可以通过放缩变成:$\left \langle w,x\right \rangle+b=±1$
在正负超平面上的俩决策临界点连线垂直三个超平面,所以有$x^+-x^-=\lambda w$
又有$\lambda=\frac{2}{||w||_2^2}$,正负超平面之间的距离就是$M=\frac 2 {||w||_2}$
现在的目标就是最大化$M$,满足
再换句话,就是求$w,b$来达到$\min\limits_w\frac{||w||^2_2}{2}$,条件是$y_i(\left \langle w,x_i\right \rangle+b)\ge 1$
过程太复杂不想写了aaaaa
等明天醒了补!
解题步骤
- 解对偶优化问题,算出$\alpha^\star$
- 用$\alpha^\star$算出$w(\alpha^\star)$和$b(\alpha^\star)$
- 用这个式子分类:$\text{sign}(\sum\limits_{i=1}^n\alpha_i^\star y_ik(x_i,x)+b(\alpha^\star))$
非线性模型
把输入空间映射到特征空间,特征空间维数越高,数据越可能线性可分。
映射完之后该咋做咋做就好了,映射用的函数叫核函数。
线性核,多项式核,高斯核
Chapter 10 - 感知机与神经网络
感知机
$f(x_i)=\text{sign}(\sum\limits_{j=0}^dw_jx_{ij})$
如果数据线性可分那就好办,否则不收敛
从一个随机的超平面开始,用训练数据来调整的迭代方法
发现$y_if(x_i)\le 0$时,更新全部$w_j=w_j+y_ix_{ij}$
感性理解,就是把每个分量拉回来对应的$x$值
$w_j$决定了$x_j$对结果的权重,可能得到很多解
神经网络
感知机用的是分段函数,换成SIGMOID,也可以换成别的激活函数比如tanh
简单的例子:用OR,NAND,AND感知机拼成XOR网络
反向传播算法
明天醒的时候再看
Chapter 11 - 决策树和朴素贝叶斯
决策树
还是做分类的。不需要实数输入,所以不需要数值化特征。
- 主要的决策:下一个用哪个标准分类?
- 用同质性作为衡量标准:如果分类两边样本数量相等同质性最高,如果分完只剩一类了那就最低。
- 熵函数 $\text{Entropy}(S)=-p_+\log p_+ -p_-\log p_-$是个关于x=0.5对称的凸函数
收获函数$\text{Gain}(S,A)=\text{Entropy}(S)-\sum\limits_{v\in\text{Value(A)}}\frac{|S_v|}{|S|}\text{Entropy}(S_v)$
把子结点人数占比作为权重,子结点熵值作为权值,父节点熵值减去子结点熵值的加权平均就是熵值收获。
很容易过拟合,两种解法:要么别长出来,要么先长出来再剪(这个更好,用一个验证集检验剪枝后有没有比之前更差)。
CART用$Gini=1-p_+^2-p_-^2$代替信息熵。
实际问题
- 先降维,保留特征性最强的特征
- 用集成方法:随机森林
- 先均衡数据集:对主要数据欠采样,对少数数据过采样
优点:
- 简单可解释
- 可以转成分类规则
- 对于分类数据很好
- 构造简单
- 不用归一化数据
缺点:
- 不稳定,一个样本不同树可能就不同
- 单变量,不处理组合特征
- 某些结点的选择可能取决于之前的选择
- 需要平衡数据
朴素贝叶斯
希望通过$p(y|x)$来找到$f(x)=y$的映射。
判别模型
对$p(y|x)$建模,然后给条决策边界来分类。
生成模型
对$p(x|y)$和$p(y)$建模,然后用贝叶斯算使得$p(y|x)=\frac{p(x|y)p(y)}{p(x)}≈p(x|y)p(y)$最大的$y$值作为结果。
输入$x$维数比较高的时候,可以默认不同维特征之间相互独立。
解题步骤
- 对每个标签$y$算$p(y)$
- 对每个标签$y$和每个特征$a_i$算$p(a_i|y)$
$m-$估计概率:$p(a_j|y)=\frac{n_c+m*p}{n_y+m}$
其中$p$是事先约定的值,不知道怎么取可以用特征$y$可能的取值数量的倒数
Chapter 12 - 集成学习与聚类
集成学习
用同样的训练数据,训练独立的弱学习者,策略有三:
- Boosting
- Bagging
- Random Forests
Boosting
在带权重的训练数据上训练弱学习者,表现好的学习者给更多权重
难样本给更高权重,简单样本给更低权重
错误率决定了最终的贡献比:
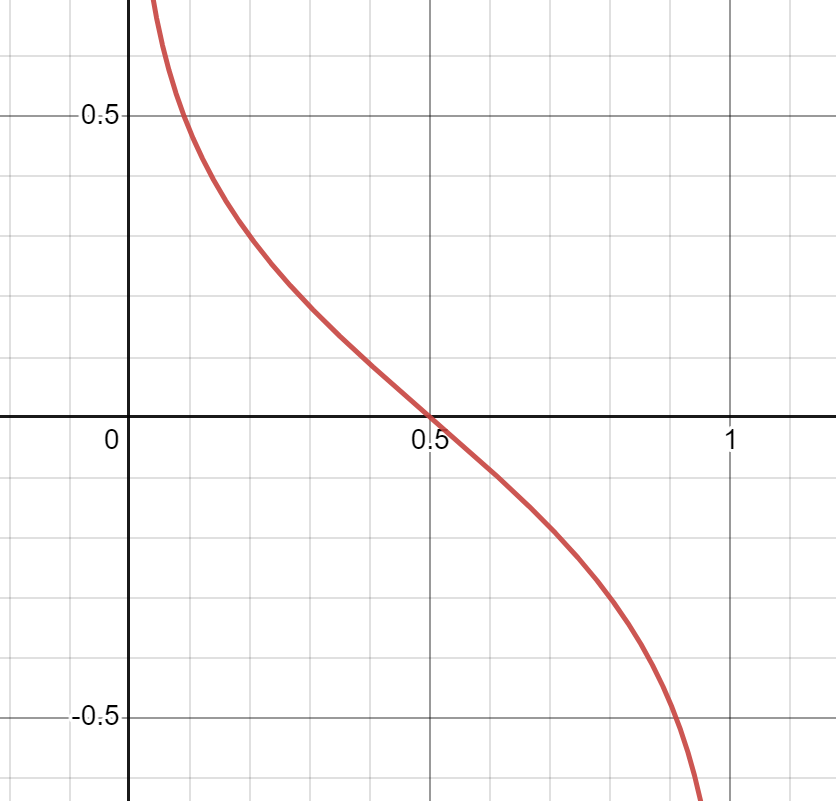
数据集上的权重从均权开始,错的人越多权值变得越大,越少就变小
Bagging
Bootstrapping是重采样,按照经验分布进行采样
Bagging和Boosting都基于Bootstrapping
都使用了重采样来生成弱分类器
Bagging = Bootstrap aggregation
每次就选等大的一部分数据用来训练一个弱分类器。
随机森林
不拆数据了,拆特征维数,每次只用一部分特征来分类,多长几棵树投票。
一般拆出来训练的特征维数$m\le\sqrt d$
聚类
无监督学习,分成$k$个聚类
K-means
最小化聚类内部的均方差:
$\mu_j$是第$j$个聚类中的平均值
优点:容易实现
缺点:得知道$K$;维数灾难;没有理论基础
K-means的一些问题
怎么取$k$?
多试几个,选”elbow-point”
G-means算法
- 用一个小$k$开始
- 从$k$个聚类中心点跑K-means
- 看看聚类是否环绕这些中心正态分布
- 如果OK就不管,如果不是那就拆成两个聚类中心
- 继续迭代,直到大家都正态分布
怎么评价模型?
内部评价:高聚类内部相似度,低聚类外部相似度数据检验,可以用 Davies-Bouldin index评估聚类的紧密型
外部评价:利用对外部数据的知识库做评估(是否符合客观规律)
如果不想要圆形聚类呢?
其他方法:spectral clustering, kernelized K-means, DBSCAN, BIRCH, etc.
怎么初始化?
K-means对聚类中心的选取高度敏感,收敛速度和聚类效果都有影响。
比较安全的技巧是新聚类中心和之前的聚类中心安排得尽量远
解决方案是多重开几次选最好的。
其他的限制?
对一些样本做硬赋值,高斯混合模型允许软赋值(不同的赋值有概率)
对离群的例子高敏感,K-median在这方面的鲁棒性更好