CS329 Machine Learning Quiz 3

Before Quiz

1. Learning

   $p(\theta\vert\mathcal D)$

   • $p(\mathcal D\vert \theta)p(\theta)$ closed-form solution
   • $L(\theta)$
     • $b=\nabla_\theta L(\theta)$
     • $H=\nabla^2_\theta L(\theta)$

   $\theta^+\leftarrow \theta - H^{-1}b$

   $p(\theta\vert\mathcal D)= \mathcal N(\theta_\text{MAP},H_\text{MAP}^{-1})$

2. Prediction

   $$p(t_{N+1}\vert x_{N+1},\mathcal D) = \int p(t_{N+1},\theta\vert x_{N+1},\mathcal D) \text d \theta = \int p(t_{N+1}\vert x_{N+1},\theta)p(\theta\vert\mathcal D)\text d \theta$$

   • $t_{N+1} = y(x_{N+1},\theta)+v$, $v\sim \mathcal N(0,\beta^{-1})$

     $p(t_{N+1}\vert x_{N+1},\mathcal D) =\mathcal N(y(x_{N+1},\theta_\text{MAP})+\bar q_\text{MAP}^\text{T}H^{-1}_\text{MAP}\bar q_\text{MAP})$

   • $y(x_{N+1},\theta)=\delta?(\Phi^\text T(x_{N+1})\theta)$

     $p(t_{N+1}\vert x_{N+1},\mathcal D) =p(t_{N+1}\vert x_{N+1},\mathcal \theta_\text{MAP}) =(y(x_{N+1},\theta_\text{MAP}))^{t_{N+1}}(1-y(x_{N+1},\theta_\text{MAP}))^{1-t_{N+1}}$

3. Evaluation

   $$\begin{align*} p(\mathcal D) &= \int p(\mathcal D\vert\theta)p(\theta)\text d \theta\\ -\ln p(\mathcal D) &=\int- \ln p(\mathcal D\vert \theta)-\ln p(\theta)\text d\theta \\ &= -\ln p(\mathcal D\vert \theta_\text{MAP})-\ln p(\theta_\text{MAP})+\int\frac 1 2 (\theta-\theta_\text{MAP})^\text T H^{-1}_\text{MAP}(\theta-\theta_\text{MAP})\text d\theta\\ &=-\ln p(\mathcal D\vert \theta_\text{MAP})-\ln p(\theta_\text{MAP})-\frac M 2 \ln(2\pi)+\frac M 2 \ln\vert H_\text{MAP} \vert \end{align*}$$

---

Question 1 Neural Networks without Prior

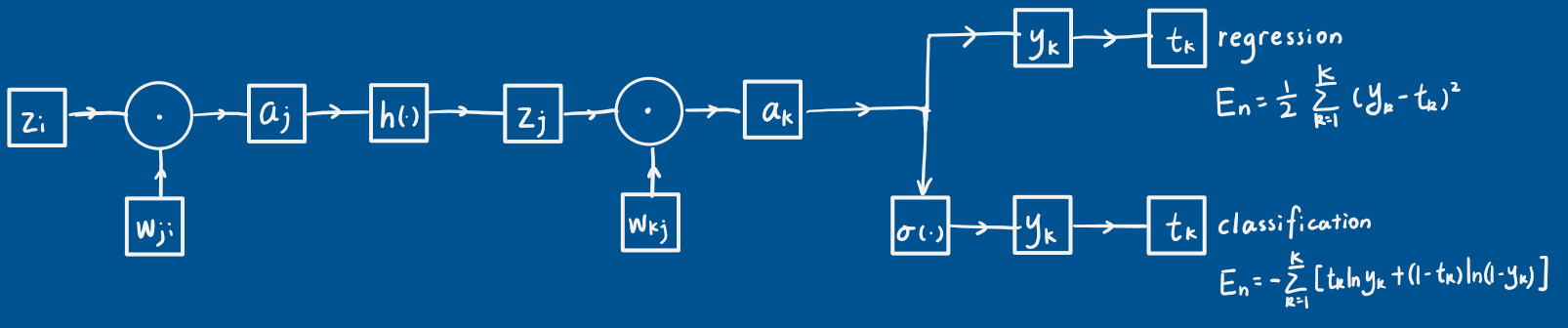
Question 1.1

What are the gradients of $\frac{\partial y_k}{\partial w_{kj}}$, $\frac{\partial y_k}{\partial w_{ji}}$ for regression and classification, respectively?

Solution 1.1

1. Regression

   $$\begin{align*} y_k&=a_k\\ \frac{\partial y_k}{\partial w_{kj}}&=\frac{\partial a_k}{\partial w_{kj}}=z_j\\ z_j&=h(a_j), \frac{\partial a_j}{\partial w_{ji}}=z_i\\ \frac{\partial y_k}{\partial w_{ji}}&=\frac{\partial a_k}{\partial z_j}\frac{\partial z_j}{\partial a_j}\frac{\partial a_j}{\partial w_{ij}}=w_{kj} h'(a_j)z_i \end{align*}$$

2. Classification

   $$\begin{align*} y_k&=\sigma(a_k)\\ \frac{\partial y_k}{\partial w_{kj}}&=\frac{\partial y_k}{\partial a_k}\frac{\partial a_k}{\partial w_{kj}}=\sigma'(a_k)z_j=y_k(1-y_k)z_j\\ z_j&=h(a_j), \frac{\partial a_j}{\partial w_{ji}}=z_i\\ \frac{\partial y_k}{\partial w_{ji}}&=\frac{\partial y_k}{\partial a_k}\frac{\partial a_k}{\partial z_j}\frac{\partial z_j}{\partial a_j}\frac{\partial a_j}{\partial w_{ij}}=y_k(1-y_k)w_{kj} h'(a_j)z_i \end{align*}$$

Question 1.2

What are the gradients of $\frac{\partial E_n}{\partial w_{kj}}$, $\frac{\partial E_n}{\partial w_{ji}}$ for regression and classification, respectively?

Solution 1.2

$$\begin{align*} \delta_k &\equiv y_k-t_k \\ \delta_j &\equiv \sum\limits_{k=1}^K\frac{\partial E_n}{\partial a_k}\frac{\partial a_k}{\partial a_j} = h'(a_j) \sum\limits_{k=1}^K w_{kj}\delta_k \\ \end{align*}$$

1. Regression

   $$\begin{align*} E_n &= \frac 1 2 \sum\limits_{k=1}^K (y_k-t_k)^2\\ \frac{\partial E_n}{\partial w_{kj}} &=\frac{\partial E_n}{\partial y_k}\frac{\partial y_k}{\partial w_{kj}} =(y_k-t_k)z_j =\delta_kz_j\\ \frac{\partial E_n}{\partial w_{ji}} &= \frac{\partial E_n}{\partial a_j}\frac{\partial a_j}{\partial w_{kj}} =h'(a_j)\sum\limits_{k=1}^N w_{kj}\delta_k z_i =\delta_jz_i \end{align*}$$

2. Classification

   $$\begin{align*} E_n &= -\sum\limits_{k=1}^K t_k\ln y_k + (1-t_k)\ln (1-y_k)\\ \frac{\partial E_n}{\partial w_{kj}} &=\frac{\partial E_n}{\partial y_k}\frac{\partial y_k}{\partial a_k}\frac{\partial a_k}{\partial w_{kj}} = (y_k-t_k)z_j = \delta_kz_j\\ \frac{\partial E_n}{\partial w_{ji}} &= \frac{\partial E_n}{\partial a_j}\frac{\partial a_j}{\partial w_{kj}} = h'(a_j)\sum\limits_{k=1}^N w_{kj}\delta_k z_i = \delta_jz_i \end{align*}$$

Question 1.3

What’s the gradients of $\frac{\partial y_k}{\partial z_i}$ for regression and classification, respectively?

Solution 1.3

1. Regression

   $$\begin{align*} \frac{\partial y_k}{\partial z_i} = \frac{\partial y_k}{\partial a_k}\frac{\partial a_k}{\partial z_j}\frac{\partial z_j}{\partial a_j}\frac{\partial a_j}{\partial z_i} = w_{kj}h'(a_j)w_{ji} \end{align*}$$

2. Classification

   $$\begin{align*} \frac{\partial y_k}{\partial z_i} = \frac{\partial y_k}{\partial a_k}\frac{\partial a_k}{\partial z_j}\frac{\partial z_j}{\partial a_j}\frac{\partial a_j}{\partial z_i} = y_k(1-y_k)w_{kj}h'(a_j)w_{ji} \end{align*}$$

Question 2 Neural Networks with Prior

If the prior of $w\sim \mathcal N(m_0,\Sigma_0^{-1})$ for both regression and classification, then

Question 2.1

What are the MAP solutions of $w,p(w\vert\mathcal D)$ for both cases?

Solution 2.1

By iterating $w^\text {new}=w^\text {old}-A^{-1}\nabla E(w)$, we obtain $w_\text{MAP}$.

1. Regression

   $$\begin{align*} E(w) &= -\ln p(w\vert \mathbf t) = \frac\alpha 2 w^\text Tw +\frac\beta 2 \sum\limits_{n=1}^N [y(x_n,w)-t_n]^2 + C\\ \nabla E(w) &=\alpha w + \beta \sum\limits_{n=1}^N (y_n-t_n)\mathbf g_n\\ \mathbf g &= \nabla_{w} y(\mathbf x,w)\vert_{w=w_\text{MAP}}\\ A&=\nabla^2 E(w) = \alpha\mathbf I + \beta \mathbf H \end{align*}$$

2. Classification

   $$\begin{align*} E(w) &= -\ln p(w\vert \mathbf t) = \frac\alpha 2 w^\text Tw -\sum\limits_{n=1}^N [t_n\ln y_n + (1-t_n)\ln(1-y_n)]\\ \nabla E(w) &=\alpha w + \sum\limits_{n=1}^N (y_n-t_n)\mathbf g_n\\ \mathbf g &= \nabla_{w} y(\mathbf x,w)\vert_{w=w_\text{MAP}}\\ A&=\nabla^2 E(w) = \alpha\mathbf I + \mathbf H \end{align*}$$

where $\mathbf H$ is the Hessian matrix of the sum of error function.

Hence we have $p(w_\text{MAP}\vert \mathcal D) = \mathcal N(w\vert w_\text{MAP},A^{-1})$.

Question 2.2

What are the predictive distributions of a new data input $x_{N+1}$ and label $t_{N+1}$ for both cases?

Solution 2.2

1. Regression

   $$p(t_{N+1}\vert x_{N+1}, \mathcal{D}) = \mathcal N(y(x,w_\text{MAP}),\beta^{-1}+g^\text T Ag)$$ $$p(t_{N+1}\vert x_{N+1},\mathcal D) =\mathcal N(y(x_{N+1},\theta_\text{MAP})+\bar q_\text{MAP}^\text{T}H^{-1}_\text{MAP}\bar q_\text{MAP})$$

1. Classification

   $$p(t_{N+1} \vert{x_{N+1}}, \mathcal{D})=\sigma\left(\kappa\left(\sigma_{a}^{2}\right) a_{M A P}\right)$$

$$p(t_{N+1}\vert x_{N+1},\mathcal D) =p(t_{N+1}\vert x_{N+1},\mathcal \theta_\text{MAP}) =(y(x_{N+1},\theta_\text{MAP}))^{t_{N+1}}(1-y(x_{N+1},\theta_\text{MAP}))^{1-t_{N+1}}$$