Outline
Propositional Logic
Predicate Logic
Mathematical Proofs
Sets
Functions
Complexity of Algorithms
Number Theory
Groups, Rings and Fields
Cryptography
Mathematical Induction
Recursion
Chapter 1 - Propositional Logic
Logical connectives:
$\neg p$,$p\vee q$,$p\wedge q$,$p\oplus q$,$p→q$,$p\leftrightarrow q$
Logical equivalence:
| Name | Content |
|---|---|
| Identity laws | $p \vee T \equiv p $,$ p \wedge F \equiv p$ |
| Domination laws | $p \wedge T \equiv T$,$p \vee F \equiv F $ |
| Idempotent laws | $p \wedge p \equiv p$ ,$p \vee p \equiv p$ |
| Double negation laws | $\neg\neg p\equiv p$ |
| Commutative laws | $p \wedge q \equiv q \wedge p$,$ p \vee q \equiv q \vee p$ |
| Associative laws | $(p \wedge q) \wedge r \equiv p \wedge (q \wedge r) $,$ (p \vee q) \vee r \equiv p \vee (q \vee r)$ |
| Distributive laws | $(p \wedge q) \vee r \equiv (p\vee r) \wedge (q \wedge r) $,$ (p \vee q) \wedge r \equiv (p\wedge r) \vee (q\wedge r)$ |
| De Morgan’s laws | $\neg(p\vee q) \equiv \neg p \wedge \neg q$,$\neg(p \wedge q)\equiv \neg p \vee \neg q$ |
| Absorption laws | $p\wedge(p\vee q) \equiv p$,$p\vee(p\wedge q)\equiv p$ |
| Negation laws | $p\vee\neg p \equiv F$,$p\wedge\neg p \equiv T$ |
| Useful law | $p→q \equiv \neg p \wedge q$ |
e.g. Show that $p → q ≡ ¬q → ¬p $ .
$\begin{aligned}
\neg q \rightarrow \neg p & \equiv \neg(\neg q) \vee(\neg p) & & \text { Useful } \\
& \equiv q \vee(\neg p) & & \text { Double negation } \\
& \equiv(\neg p) \vee q & & \text { Communtative } \\
& \equiv p \rightarrow q & & \text { Useful }
\end{aligned}$
Rules of Inference:
| modus ponens | modus tollens | hypothetical syllogism | disjunctive syllogism |
|---|---|---|---|
| $\begin{array}{r}p \rightarrow q \\p \\\hline \therefore q\end{array}$ | $\begin{array}{r}p \rightarrow q \\\ \neg q\\\hline \therefore \neg p\end{array}$ | $\begin{array}{r}p \rightarrow q \\q \rightarrow r \\\hline \therefore p \rightarrow r\end{array}$ | $\begin{array}{r}p \vee q \\\neg p\\\hline \therefore q\end{array}$ |
| Addition | Simplification | Conjunction | Resolution |
| $\begin{array}{r}p\\\hline\therefore p\vee q\end{array}$ | $\begin{array}{r}p\wedge q\\\hline\therefore q\end{array}$ | $\begin{array}{r}p\\q\\\hline\therefore p\wedge q\end{array}$ | $\begin{array}{r}\neg p\vee r\\p\vee q\\\hline\therefore q\vee r\end{array}$ |
Chapter 2 - Predicate Logic
Truth set:$\{(x_1,x_2,\cdots,x_n)\in D|P(x_1,x_2,\cdots,x_n)=T\}$
Quantifier: $\forall$(Universal), $\exists$(Existential)
De Morgan laws for quantifiers:
$\neg\exists P(x)\equiv \forall\neg P(x)$,$\neg\forall P(x)\equiv\exists\neg P(x)$
Order of Quantifiers:
- matters if quantifiers are of different type
- does no matter if quantifiers are of the same type
Negating Nested Quantifiers:
Swap every quantifier, and negation the inner proposition.
Rules of Inference:
| Universal Instantiation | Universal Generalization | Existential Instantiation | Existential Generalization |
|---|---|---|---|
| $\begin{array}{r}\forall xP(x)\\\hline\therefore P(c)\end{array}$ | $\begin{array}{r}P(c)\text{ for an arbitrary }c\\\hline\therefore \forall x P(x)\end{array}$ | $\begin{array}{r}\exists x P(x)\\\hline\therefore P(c)\text{ for some element }c\end{array}$ | $\begin{array}{r}P(c)\text{ for some element }c\\\hline\therefore \exists x P(x)\end{array}$ |
Chapter 3 - Mathematical Proofs
Methods of Proving Theorems:
- direct proof
- $p → q$ is proved by showing that if $p$ is true then $q$ follows
- proof by contrapositive
- show the contrapositive $¬q → ¬p$
- proof by contradiction
- show that $(p ∧ ¬q)$ contradicts the assumptions
- proof by cases
- give proofs for all possible cases
proof of equivalence
- $p ↔ q$ is replaced with $(p → q) ∧ (q → p)$
vacuous proof
- $p→q$ is always true if $p$ (the hypothesis) is always false
- trivial proof
- $p→q$ is always true if $q$ (the conclusion) is always true
Proofs with Quantifiers:
Universal
prove the property holds for all examples
– proof by cases to divide the proof into different parts
counterexamples
– disprove universal statement
Existential
constructive
– find a specific example to show the statement holds
nonconstructive
– proof by contradiction
Chapter 4 - Sets
Important sets:
$\mathbf {N, Z, Z^+, Q, R, C}$
Russell’s Paradox:
Let $S=\{x|x\notin x\}$, is a set of sets that are not member of themselves. Is $S\in S$ or $S\notin S$?
Set Operations:
$A\times B, A\cup B,A\cap B,\bar{A},A-B$
Cardinality:
The sets $A$ and $B$ have the same cardinality if there is a bijection between elements in $A$ and $B$.
$|A|\le|B|$ if there is an injection from $A$ to $B$, if they have different cardinalities then $|A|<|B|$.
Countable Sets:
A set that is either finite or has the same cardinality as the set of $\mathbf Z^+$ is called countable.
Cantor diagonalization argument:
“Every part is different from some of the previous ones.”
Schröder-Bernstein Theorem:
$|A|\le |B|$, $|B|\le |A|$, then $|A|=|B|$.
Cantor’s Theorem:
If $S$ is a set, then $|S| < |\mathcal P(S)|$ .
Chapter 5 - Functions
Functions:
A function from $A$ to $B$, denoted by $f : A → B$, is an assignment of exactly one element of $B$ to each element of $A$.
domain, codomain, image, preimage, range.
Injective (One-to-one) Function
Surjective (Onto) Function
Bijective (One-to-one Correspondence) Function
Invert Function (Exists IFF bijection)
Composition of Functions
Sequence:
A sequence is a function from a subset of the set of integers.
arithmetic progression, geometric progression
Some Useful Summation Formulas:
| Sum | Closed Form |
|---|---|
| $\sum\limits_{k=0}^{n}ar^k(r\ne0,1)$ | $\frac{ar^{n+1}-a}{r-1}$ |
| $\sum\limits_{k=1}^{n}k$ | $\frac{n(n+1)}{2}$ |
| $\sum\limits_{k=1}^{n}k^2$ | $\frac{n(n+1)(2n+1)}{6}$ |
| $\sum\limits_{k=1}^{n}k^3$ | $\frac{n^2(n+1)^2}{4}$ |
| $\sum\limits_{k=0}^{\infty}x^k,-1<x<1$ | $\frac{1}{1-x}$ |
| $\sum\limits_{k=1}^{\infty}kx^{k-1},-1<x<1$ | $\frac{1}{(1-x)^2}$ |
Chapter 6 - Complexity of Algorithms
Big-O Notation:
$f(n)=O(g(n))$, if $\exists C>0,x_0>0$ s.t. $\forall n>x_0,\ |f(n)|\le C|g(n)|$
Combinations of Functions:
$(f_1+f_2)(x)=O(\max(|g_1(x)|,|g_2(x)|))$
$(f_1f_2)(x)=O(g_1(x)g_2(x))$
Big-Omega Notation:
$f(n)=\Omega(g(n))$, if $\exists C>0,x_0>0$ s.t. $\forall n>x_0, |f(n)|\ge C|g(n)|$
$f(n)=O(g(n))$ IFF $g(n)=\Omega(f(n))$
Big-Theta Notation:
$f(n)=\Theta(g(n))$, if $f(n)=O(g(n))$ and $g(n)=O(f(n))$
The Input Size of Problems:
The input size of a problem is the minimum number of bits ($\{0,1\}$) needed to encode the input of the problem.
Same type functions:
Two positive functions $f(n)$ and $g(n)$ are of the same type if
for all large $n$, where $a_1,b_1,c_1,a_2,b_2,c_2$ are some positive constants.
All polynomials are of the same type, but polynomials and exponentials are of different types.
Polynomial-Time Algorithms:
An algorithm is polynomial-time if its running time is $O(n^k)$, where $k$ is a constant independent of $n$, and $n$ is the input size of the problem that the algorithm solves.
The class P:
The class P consists of all decision problems that are solvable in polynomial time. That is, there exists an algorithm that will decide in polynomial time if any given input is a yes-input or a no-input.
The class NP:
The class NP consists of all decision problems such that, for each yes-input, there exists a certificate which allows one to verify in polynomial time that the input is indeed a yes-input.
Reduction:
Problem $Q$ can be reduced to $Q’$ if every instance of $Q$ can be “rephrased” to an instance of $Q’$.
“$Q$ is no harder to solve than $Q’$”
Polynomial-Time Reductions:
$f$ transforms an input $x$ for $L_1$ into an input $f(x)$ for $L_2$
$f$ is computable in polynomial time in size($x$)
If such an $f$ exists, we say that $L_1$ is polynomial-time reducible to $L_2$, and write $L_1 \le_P L_2$.
“$L_1$ is no harder than $L_2$”
Polynomial-Time Reduction $f : L_1 → L_2$:
If $L_1\le_P L_2$ and $L_2\in P$, then $L_1\in P$.
If $L_1\le_P L_2$, $L_2\le_P L_3$, then $L_1\le_P L_3$.
The class NP-Complete:
- $L\in NP$
- $\forall L’\in NP$, $L’\le_P L$
$NPC$ consists of all the hardest problems in $NP$.
NP-Completeness and Its Properties:
Let $L$ be any problem in $NPC$.
If there is a polynomial-time algorithm for $L$, then there is a polynomial-time algorithm for every $L’\in NP$
If there is no polynomial-time algorithm for $L$, then there is no polynomial-time algorithm for every $L’\in NPC$
Either all NP-Complete problems are polynomial time solvable, or all NP-Complete problems are not polynomial time solvable.
Chapter 7 - Number Theory
Properties of Divisibility:
- if $a|b$ and $a|c$, then $a|(b+c)$
- if $a|b$ then $a|bc$ for all integers $c$
- if $a|b$ and $b|c$, then $a|c$
Congruence Relation:
$a\equiv b\mod m$ IFF $m|(a-b)$
$a\equiv b\mod m$ IFF $a\mod m = b\mod m$
If $a\equiv b \mod m$ and $c\equiv d\mod m$, then $a+c\equiv b+d \mod m$ and $ac\equiv bd\mod m$
$(a+b)\mod m=((a\mod m)+(b\mod m))\mod m$
$ab\mod m=((a\mod m)(b\mod m))\mod m$
Arithmetic Modulo m:
$(\mathbf Z_m,+_m,\cdot_m)$
Closure: if $a,b\in \mathbf Z_m$, then $a+_mb,a\cdot_mb\in \mathbf Z_m$
Associativity: if $a,b,c\in \mathbf Z_m$, then
$(a+_mb)+_mc=a+_m(b+_mc)$
$(a\cdot_mb)\cdot_mc=a\cdot_m(b\cdot_mc)$
Identity elements: $a+_m0=a$ and $a\cdot_m1=a$
Additive inverses: if $a\ne0$ and $a\in \mathbf Z_m$, then $m-a$ is an additive inverse of $a$ modulo $m$
Commutativity: if $a,b\in \mathbf Z_m$, then $a+_mb=b+_ma$
Distributivity: if $a,b,c\in \mathbf Z_m$, then
$a\cdot_m(b+_mc)=(a\cdot_mb)+_m(a\cdot_mc)$
$(a+_mb)\cdot_mc=(a\cdot_mc)+_m(b\cdot_mc)$
Group:
$(G,\star)$
- Closure
- Associativity
- Identity element
- Inverse
e.g. Permutation Group:$(P_n,\circ )$
Abelian Group:
$(G,\star)$
- Group
- Commutativity
Ring:
$(R,+,\times)$
- Abelian Group $(R,+)$
- Associativity of $\times$
- Distributivity
Commutative Ring:
$(R,+,\times)$
- Ring
Commutativity of $\times$
Integral Domain:
$(R,+,\times)$
- Commutative Ring
- Identity element of $\times$
- Nonzero product
Field:
$(\mathbb F,+,\times)$
- Integral Domain
- Inverse of $\times$
Prime Field and Characteristic:
Consider a finite field $\mathbb F$, define
$S_r=1+1+\cdots+1$ as sum of $r$ 1’s for a positive integer $r$.
Let $p$ be the smallest positive number with $S_p=0$.
If such a $p$ exists, it must be prime.
If $p=a\cdot b$ with $0<a,b<p$, then by distributivity, $0=S_p=S_a\cdot S_b$. Then one of $S_a,\ S_b$ must be 0, contradicting the minimality of $p$.
This $p$ is called the characteristic of the field $\mathbb F$.
The subset $\{0,S_1,S_2,\cdots,S_{p-1}\}$ is isomorphic to $\mathbb F$(prime field).
Any finite field $\mathbb F$ is a finite dimensional vector space over $\mathbb F_p$, with $n=dim_{\mathbb F_p}(\mathbb F)$, $|\mathbb F|=p^n$, i.e., the cardinality of $\mathbb F$ must be a prime power.
Uniqueness of finite fields:
For any prime power $q$, there is essentially only one finite field of order $q$. Any two finite fields of order $q$ are the same except that the labelling used to represent the field elements may be different.
Binary field:
characteristic-2 finite fields $\mathbb F_{2^m}$
Elements are polynomials over $\mathbb F_2$ of degree $\le m-1$
$\mathbb F_{2^m}:=\{a_{m-1}x^{m-1}+a_{m-2}x^{m-2}+\cdots+a_2x^2+a_1x+a_0:\ a_i\in \mathbb F_2\}$
An irreducible polynomial $f (x)$ of degree $m$ is chosen:
$f (x)$ cannot be factered as a product of binary polynomials each of degree less than $m$
- Addition: usual
- Multiplication: modulo $f(x)$
| $\alpha^{0}=1$ | $\alpha^{1}=\alpha$ | $\alpha^{2}$ | $\alpha^3$ |
|---|---|---|---|
| $\alpha^{4}=\alpha+1$ | $\alpha^{5}=\alpha^{2}+\alpha$ | $\alpha^{6}=\alpha^{3}+\alpha^{2}$ | $\alpha^{7}=\alpha^{3}+\alpha+1$ |
| $\alpha^{8}=\alpha^{2}+1$ | $\alpha^{9}=\alpha^{3}+\alpha$ | $\alpha^{10}=\alpha^{2}+\alpha+1$ | $\alpha^{11}=\alpha^{3}+\alpha^{2}+\alpha$ |
| $\alpha^{12}=\alpha^{3}+\alpha^{2}+\alpha+1$ | $\alpha^{13}=\alpha^{3}+\alpha^{2}+1$ | $\alpha^{14}=\alpha^{3}+1$ | $\alpha^{15}=1$ |
$<\alpha^3,\alpha^2,\alpha,1>$ is a basis for $\mathbb F_{2^4}$ over $\mathbb F_2$.
The finite field $\mathbb F_{q^n}$ can be viewed as a vector space over $\mathbb F_q$.
Isomorphism of Finite Fields:
For a fixed $q$, the finite field $\mathbb F_q$ is unique.
if $\psi: z\mapsto c$ is an isomorphism between $K_1$ and $K_2$, then $f_1(c)\equiv 0\mod f_2(c)$ for some $c\in K_2$.
Extension Fields and Subfields:
Let $p$ be a prime and $m\ge2$. Let $\mathbb F_p[z]$ denote the set of all polynomials in the variable $z$ with coefficients from $\mathbb F_p$. Let $f(z)$ be an irreducible polynomial of degree $m$ in $\mathbb F_p[z]$.
The elements of $\mathbb F_{p^m}$ are the polynomials in $\mathbb F_p[z]$ of degree $\le m-1$:
- Addition: usual addition of polynomials, with coefficients arithmetic performed in $\mathbb F_p$.
- Multiplication: performed modulo the polynomial $f(z)$.
A finite field $\mathbb F_{p^m}$ has precisely one subfield of order $p^ℓ$ for each positive divisor $ℓ$ of $m$.
The elements of this subfield are the elements $a\in \mathbb F_{p^m}$ satisfying $a^{p^ℓ}=a$; Conversely, every subfield of $\mathbb F_{p^m}$ has order $p^ℓ$ for some positive divisor $$
Base-b Expansions :
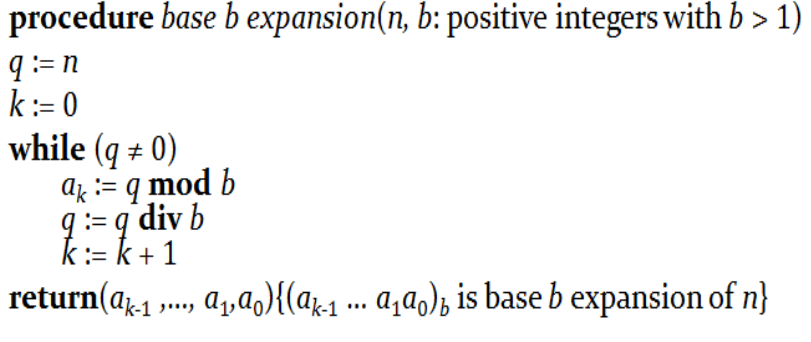
$O(\log n)$
Binary Addition of Integers
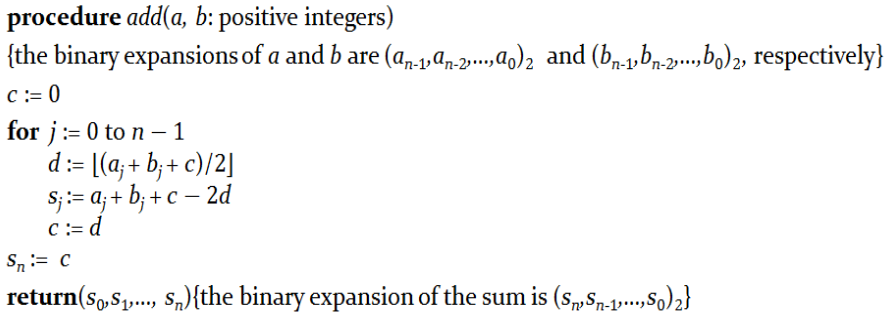
$O(n)$ bit additions
Binary Multiplication of Integers

$O(n^2)$ shifts and $O(n^2)$ bit additions
Computing div and mod

$O(\log q\log a)$ bit operations
Binary Modular Exponentiation:

$O((\log m)^2\log n)$ bit operations
Primes & Composites:
If $n$ is composite, then $n$ has a prime divisor less than or equal to $\sqrt n$.
if $n$ is composite, then it has a positive integer factor a such that $1 < a < n$ by definition. This means that $n = ab$, where $b$ is an integer greater than 1.
assume that $a>\sqrt n$ and $b>\sqrt n$. Then ab > n, contradiction. So either $a\le \sqrt n$ or $b\le \sqrt n$.
Thus, $n$ has a divisor less than $\sqrt n$.
By the Fundamental Theorem of Arithmetic, this divisor is either prime, or is a product of primes. In either case, n has a prime divisor less than $\sqrt n$.
There are infinitely many primes.
- assume that there are finite primes $\{a_n\}$, where $a_n$ is the largest one.
- then we construct $a_{n+1}=(\prod\limits_{i=1}^{n}a_i)+1$
- $a_{n+1}$ cannot be divided by any primes smaller than itself, so it is a prime number larger than $a_n$, contradiction.
GCD & LCM Using Factorization:
$a=\prod\limits_{i=1}^{n}p_i^{a_i}$, $b=\prod\limits_{i=1}^{n}p_i^{b_i}$
$gcd(a,b)=\prod\limits_{i=1}^{n}p_i^{min(a_i,b_i)}$
$lcm(a,b)=\prod\limits_{i=1}^{n}p_i^{max(a_i,b_i)}$
Euclidean algorithm ($O(\log b)$):

Lemma Let $a=bq+r$, where $a,b,q,r$ are integers. Then $gcb(a,b)=gcd(b,r)$
- Suppose $d|a$ and $d|b$, then $d|(a-bq)$ i.e. $d|r$.
- Suppose $d|b$ and $d|r$, then $d|(bq+r)$ i.e. $d|a$.
Therefore, $gcd(a,b)=gcd(b,r)$.
Bezout’s Theorem:
If $a$ and $b$ are positive integers, then there exist integers $s$ and $t$ such that $gcd(a,b)=sa+tb$.
$\begin{aligned}
503 & = 1 \cdot 286+217 \\
286 & = 1 \cdot 217+69 \\
217 & = 3 \cdot 69+10 \\
69 & = 6 \cdot 10+9 \\
10 & = 1 \cdot 9+1
\end{aligned}$
$\begin{aligned}
1 & =10-1 \cdot 9 \\
& =7 \cdot 10-1 \cdot 69 \\
& =7 \cdot 217-22 \cdot 69 \\
& =29 \cdot 217-22 \cdot 286 \\
& =29 \cdot 503-51 \cdot 286
\end{aligned}$
Corollaries of Bezout’s Theorem:
If $a,b,c$ are positive integers such that $gcd(a,b)=1$ and $a|bc$, then $a|c$.
- $1=sa+tb$, $c=sac+tbc$, $a|bc$, $a|(sac+tbc)$, i.e. $a|c$.
If $p$ is prime and $p|\prod\limits_{i=1}^n a_i$, then $p|a_i$ for some $i$.
- by induction. Will be given later
Uniqueness of Prime Factorization:
Suppose that the positive integer $n$ can be written as a product of primes in 2 distinct ways:
$n=\prod\limits_{i=1}^sp_i$ and $n=\prod\limits_{j=1}^t q_j$
Remove all common primes from the factorizations to get
$\prod\limits_{k=1}^{u}p_{i_k}=\prod\limits_{k=1}^{v}q_{j_k}$
It then follows that $p_{i_1}|q_{j_k}$ for some $k$, contradicting the assumption that $p$ and $q$ are distinct primes.
Dividing Congruences by an Integer:
Let $m$ be a positive integer and let $a,b,c$ be integers. If $ac\equiv bc\mod m$ and $gcd(c,m)=1$, then $a\equiv b \mod m$.
Modular Inverse:
An integer $\bar a$ such that $\bar aa\equiv 1 \mod m$ is said to be an inverse of $a$ modulo $m$
If $a$ and $m$ are relatively prime integers and $m>1$, then and inverse of $a$ modulo $m$ exists. Furthermore, the inverse is unique modulo $m$.
Existence: $gcd(a,m)=1$, $sa+tm=1$, $sa+tm\equiv 1\mod m$, $sa\equiv 1\mod m$.$s$ is an inverse of $a$ modulo $m$.
Uniqueness: $sa\equiv 1\mod m$, $ta\equiv 1 \mod m$, $(t-s)a\equiv 0\mod m$, $a\mod m\ne0$, so $(s-t)\equiv 0 \mod m$. Since $s,t\in\mathbf Z_m$, $s-t=0$, i.e. $s=t$
Find inverses: extended Euclidean algorithm:
$\begin{align}
4620 & = 45 \cdot 101+75 \\
101 & = 1 \cdot 75+26 \\
75 & = 2 \cdot 26+23 \\
26 & = 1 \cdot 23+3 \\
23 & = 7 \cdot 3+2 \\
3 & = 1 \cdot 2+1 \\
2 & = 2 \cdot 1
\end{align}$
$\begin{aligned}
1 & =3-1 \cdot 2 \\
1 & =3-1 \cdot(23-7 \cdot 3)=-1 \cdot 23+8 \cdot 3 \\
1 & =-1 \cdot 23+8 \cdot(26-1 \cdot 23)=8 \cdot 26-9 \cdot 23 \\
1 & =8 \cdot 26-9 \cdot(75-2 \cdot 26)=26 \cdot 26-9 \cdot 75 \\
1 & =26 \cdot(101-1 \cdot 75)-9 \cdot 75 \\
& =26 \cdot 101-35 \cdot 75 \\
1 & =26 \cdot 101-35 \cdot(4620-45 \cdot 101) \\
& =-35 \cdot 4620+1601 \cdot 101
\end{aligned}$
Number of Solutions to Congruences:
Let $d = gcd(a, m)$ and $m’ = m/d$. The congruence $ax \equiv b \mod m$ has solutions if and only if $d|b$. If $d|b$, then there are exactly $d$ solutions. If $x_0$ is a solution, then the other solutions are given by $x_0 + m’ , x_0 + 2m’ ,\cdots, x_0 + (d − 1)m’ $.
- “only if”: If $x_0$ is a solution, then $ax_0-b=km$. Thus, $ax_0-km=b$, Since $d|(ax_0-km)$, we must have $d|b$.
- “if”: Suppose that $d|b$. Let $b=kd$. There exist integers $s,t$ such that $d=sa+tm$. Then $b=kd=ask+mtk$. Let $x_0=sk$, then $ax_0\equiv b\mod m$.
- “#=d”: $m|a(x_1-x_0)$, and $m’|a’(x_1-x_0)$, $x_1=x_0+km’$, where $k=0,1,\cdots,d-1$.
The Chinese Remainder Theorem:
$\{m_n\}$ are pairwise relatively prime positive integers greater than 1 and $\{a_n\}$ be arbitrary integers. Then the system
has a unique solution modulo $m=\prod\limits_{i=1}^{n}m_i$.
Let $M_k=m/m_k$ for $k=1,2,\cdots,n$ and $m=\prod\limits_{i=1}^{n}m_i$. Since $gcd(m_k,M_k)=1$, there is an integer $y_k$, an inverse of $M_k$ modulo $m_k$ such that $M_ky_k\equiv 1\mod m_k$. Let
It is checked that $x$ is a solution to the $n$ congruences.
Uniqueness: Suppose there are two solutions $u$ and $v$ to the system, then $m_i|(u-v),\ i=1,2,\cdots,n$, then $m|(u-v)$, i.e. $u\equiv v\mod m$.
Back Substitution:
……
Pseudorandom Number Generators:
$x_{n+1}=(ax_n+c)\mod m$
Hash Functions:
……
Chapter 8 - Cryptography
Fermat’s Little Theorem:
Let $p$ be a prime, and let $x$ be an integer such that $x\not\equiv0\mod p$. Then $x^{p-1}\equiv 1\mod p$.
Proof of Fermat’s Little Theorem:
Lemma(Dividing Congruences by an Integer)
Let $m$ be a positive integer and let $a,b,c$ be integers. If $ac\equiv bc\mod m$ and $gcd(c,m)=1$, then $a\equiv b \mod m$.
- Pick distinct $u,v$ from $\mathbf Z_m$, suppose $ux\equiv vx \mod m$, $gcd(x,m)=1$, then $u\equiv v\mod m$, contradiction.
- So $\{1,2,\cdots,p-1\}=\{x,2x,\cdots,(p-1)x \mod p\}$
- $(p-1)!x^{p-1}\equiv(p-1)!\mod p$
- Since $gcd((p-1)!,p)=1$, $x^{p-1}\equiv 1\mod m$
Euler’s totient function:
$\phi(n)$: the number of positive integers coprime to $n$ in $\mathbf Z_m$.
For prime numbers $p$
$\phi(p)=p-1$
$\phi(p^i)=p^i-p^{i-1}$
For positive integer $n>1$, it has factorization $n=p_1^{k_1}p_2^{k_2}\cdots p_r^{k_r}$
- $\phi(n)=\prod\limits_{i=1}^{r}(p^{k_i}-p^{k_i-1})$
- $m>1$ and $gcd(m,n)=1$,$\phi(mn)=\phi(m)\phi(n)$
Euler’s Theorem:
Let $n$ be a positive integer, and let $x$ be an integer such that $gcd(x,n)=1$. Then
Denote the set of numbers coprime to n in $\mathbf Z_n$ as $\{X_{\phi(n)}\}$.
Pick $u,v$ from $\{X_{\phi(n)}\}$, suppose $ux\equiv vx\mod n$, $gcd(x,n)=1$, then $u\equiv v\mod n$.
So the cardinality $|\{X_{\phi(n)}\}|=|\{x\cdot X_{\phi(n)}\}|$
Now prove that for $X_i\in\{X_{\phi(n)}\}$, $gcd(x\cdot X_i,n)=1$.
Assume that $x\cdot X_i\equiv r \mod n$, and $t=gcd(r,n)\ne1$, i.e. $x\cdot X_i=kn+r$
Since $t|n,\ t|r$, $t|x\cdot X_i$, $gcd(X_i, n)=1$
So $t|x$, $gcd(x,n)\ge t>1$, contradiction.
So multiplying $x$ to $\{X_{\phi(n)}\}$ is actually a bijection $f: \{X_{\phi(n)}\}→\{X_{\phi(n)}\}$
$\prod\limits_{i=1}^{\phi(n)}x\cdot X_i\equiv\prod\limits_{i=1}^{\phi(n)}X_i\mod n$
Eliminate the product of $X_i$ (which is coprime to n), we get $x^{\phi(n)}\equiv 1\mod n$
Primitive Roots:
There is a primitive root modulo $n$ IFF $n=2,4,p^e \text{ or }2p^e$,where $p$ is an odd prime.
If $n$ has primitive roots, then it has $\phi(\phi(n))$ primitive roots.
RSA Public Key Cryptosystem:
Pick two large primes $p$ and $q$. Let $n=pq$, then $\phi(n)=(p-1)(q-1)$. Encryption and decryption keys $e$ and $d$ are selected such that
- $gcd(e,\phi(n))=1$
- $ed\equiv 1\mod \phi(n)$
RSA encryption: $C=M^e\mod n$
RSA decryption: $M=C^d\mod n$
For each integer $x$ such that $0\leq x<n$, $x^{ed}\equiv x\mod n$.
$p,q,\phi(n)$ must be kept secret!
Let $(e,d)$ be a key pair for the RSA. Define $\lambda(n)=lcm(p-1,q-1)$, and compute $d’=e^{-1}\mod \lambda(n)$, decryption using $d’$ still works!
Discrete Logarithm Problem:
For $b^x\equiv y\mod n$, given $n$, $b$ and $y$, find $x$. This is very hard!
El Gamal Encryption:
……
Chapter 9 - Mathematical Induction
Proof by Smallest Counterexample:
The statement $P(n)$ is true for all $n=0,1,2,\cdots$
- Assume that a counter-example exists, i.e. there is some $n>0$ for which $P(n)$ is false.
- Let $m>0$ be the smallest value for which $P(m)$ is false.
- Then use the fact that $P(m’)$ is true for all $0\le m’<m$ to show that $P(m)$ is true, contradicting the choice of $m$.
Weak Principle of Mathematical Induction:
Base step: If the statement $P(b)$ is true.
Inductive step: The statement $P(n-1)→P(n)$ is true for all $n>b$, then $P(n)$ is true for all integers $n\ge b$.
Strong Principle of Mathematical Induction:
Base step: If the statement $P(b)$ is true.
Inductive step: The statement $P(b)\wedge P(b+1)\wedge \cdots\wedge P(n-1)→P(n)$ is true for all $n>b$, then $P(n)$ is true for all integers $n\ge b$.
Weak 々 is equivalent to Strong 々.
Chapter 10 - Recursion
Iterating a Recurrence:
“Top-down”: $T(n)=rT(n-1)+a=r(rT(n-2)+a)+a=\cdots$
“Bottom-up”: $T(0)=b,\ T(1)=rT(0)+a,\ T(2)=rT(1)+a\cdots$
Formula of Recurrences:
$T(n)=rT(n-1)+a,\ T(0)=b$, and $r\ne1$,
then
for all nonnegative integers $n$.
First-Order Linear Recurrences:
$T(n)=f(n)T(n-1)+g(n)$
When $f(n)$ is a constant:
The Master Theorem:
$T(n)=aT(n/b)+cn^d$
- If $a<b^d$, then $T(n)=\Theta(n^d)$
- If $a=b^d$, then $T(n)=\Theta(n^d\log n)$
- If $a>b^d$, then $T(n)=\Theta(n^{\log_ba})$
